
如图所示,已知AD与BC相交于E,∠1=∠2=∠3,BD=CD,∠ADB=90°,CH⊥AB于H,CH交AD于F.
(1)求证:CD∥AB;
(2)求证:△BDE≌△ACE;
(3)若O为AB中点,求证:OF=![]() BE.
BE.
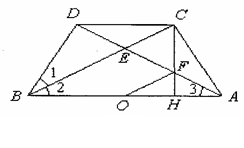 |
证明:(1)∵BD=CD,∴∠BCD=∠1.∵ ∠l=∠2,∠BCD=∠2.∴CD∥AB.
(2) ∵ CD∥AB ∴∠CDA=∠3.
∠BCD=∠2=∠3.且BE=AE.且∠CDA=∠BCD.∴DE=CE.
在△BDE和△ACE中, DE=CE,∠DEB=∠CEA,BE=AE.∴△BDE≌△ACE
 (3) ∵△BDE≌△ACE
(3) ∵△BDE≌△ACE
∠4=∠1,∠ACE=∠BDE=90°.
∴∠ACH=90°一∠BCH
又CH⊥AB,.∴ ∠2=90°一∠BCH
∴∠ACH=∠2=∠1=∠4.AF=CF
∵∠AEC=90°一∠4,∠ECF=90°一∠ACH
∠ACH=∠4 ∠AEC=∠ECF.CF=EF.∴ EF=AF
O为AB中点,OF为△ABE的中位线 ∴OF=![]() BE
BE


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源:中学学习一本通 数学 七年级下册 人教课标 题型:044
| |||||||||||
查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com