
 在△ABC中,∠C=90,AD是∠BAC的平分线,BC为切线,DB=5,CD=3,求:AC的长.
在△ABC中,∠C=90,AD是∠BAC的平分线,BC为切线,DB=5,CD=3,求:AC的长.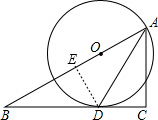 解:过D作DE⊥AB于E,
解:过D作DE⊥AB于E,
|


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,点M,P,N,Q分别在AO,BO,CO,DC上,且AM=BP=CN=DQ.求证:四边形MPNQ是矩形.
已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,点M,P,N,Q分别在AO,BO,CO,DC上,且AM=BP=CN=DQ.求证:四边形MPNQ是矩形.查看答案和解析>>
科目:初中数学 来源: 题型:
 (黑线表示被弟弟涂掉的部分),请你将这道作业题补充完整,并列方程解答.
(黑线表示被弟弟涂掉的部分),请你将这道作业题补充完整,并列方程解答.查看答案和解析>>
科目:初中数学 来源: 题型:
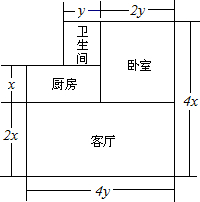 已知房屋的高度为h m,现老板娘在客厅和卧室的墙壁上贴壁纸,那么至少需要多少平方米的壁纸?如果某种壁纸的价格是b元/m2,那么购买所需壁纸至少需要多少元?(计算时不扣除门,窗所占的面积)
已知房屋的高度为h m,现老板娘在客厅和卧室的墙壁上贴壁纸,那么至少需要多少平方米的壁纸?如果某种壁纸的价格是b元/m2,那么购买所需壁纸至少需要多少元?(计算时不扣除门,窗所占的面积)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com