
【题目】如图,函数y=![]() (x<0)的图象与直线y=
(x<0)的图象与直线y=![]() x+m相交于点A和点B.过点A作AE⊥x轴于点E,过点B作BF⊥y轴于点F,P为线段AB上的一点,连接PE、PF.若△PAE和△PBF的面积相等,且xP=﹣
x+m相交于点A和点B.过点A作AE⊥x轴于点E,过点B作BF⊥y轴于点F,P为线段AB上的一点,连接PE、PF.若△PAE和△PBF的面积相等,且xP=﹣![]() ,xA﹣xB=﹣3,则k的值是( )
,xA﹣xB=﹣3,则k的值是( )
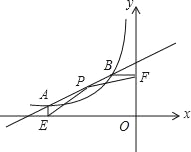
A. ﹣5 B. ![]() C. ﹣2 D. ﹣1
C. ﹣2 D. ﹣1
科目:初中数学 来源: 题型:
【题目】1955年,印度数学家卡普耶卡(![]() )研究了对四位自然数的一种变换:任给出四位数
)研究了对四位自然数的一种变换:任给出四位数![]() ,用
,用![]() 的四个数字由大到小重新排列成一个四位数
的四个数字由大到小重新排列成一个四位数![]() ,再减去它的反序数
,再减去它的反序数![]() (即将
(即将![]() 的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数
的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数![]() ,然后继续对
,然后继续对![]() 重复上述变换,得数
重复上述变换,得数![]() ,…,如此进行下去,卡普耶卡发现,无论
,…,如此进行下去,卡普耶卡发现,无论![]() 是多大的四位数,只要四个数字不全相同,最多进行
是多大的四位数,只要四个数字不全相同,最多进行![]() 次上述变换,就会出现变换前后相同的四位数
次上述变换,就会出现变换前后相同的四位数![]() ,这个数称为
,这个数称为![]() 变换的核.则四位数9631的
变换的核.则四位数9631的![]() 变换的核为______.
变换的核为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ![]() ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
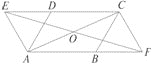
(1)求证:四边形AFCE是平行四边形.
(2)若去掉已知条件的“∠DAB=60°,上述的结论还成立吗 ”若成立,请写出证明过程;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面中,两条直线相交有一个交点,三条直线两两相交最多有3个交点,四条直线两两相交最多有6个交点……由此猜想,当相交直线的条数为n时,最多可有的交点数m与直线条数n之间的关系式为:m=_____.(用含n的代数式填空)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
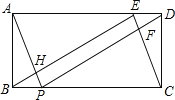
【题目】如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.
(1) 判断△BEC的形状,并说明理由;
(2) 求证:四边形EFPH是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABOC的顶点A的坐标为(-4,5),D是OB的中点,E是OC上的一点,当△ADE的周长最小时,点E的坐标是( )
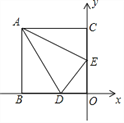
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 与反比例函数
与反比例函数![]() 的图象在第一、第三象限分别交于
的图象在第一、第三象限分别交于![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点.
两点.
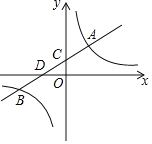
(1)求一次函数和反比例函数的解析式;
(2)比较大小:![]()
![]() ;
;
(3)求出![]() 时,
时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=9,BC=6,AD为BC边上的高,过点A作AE//BC,过点D作DE//AC,AE与DE交于点E,AB与DE交于点F,连结BE.
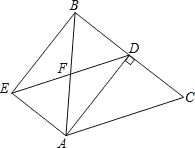
求证:(1)四边形AEBD是矩形;(2)求四边形AEBD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com