
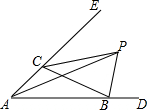
 如图,在△ABC中,点P是△ABC的外角∠DBC、∠BCE的平分线的交点,若∠BPC=72°,连接AP,则∠BAP=18 度.
如图,在△ABC中,点P是△ABC的外角∠DBC、∠BCE的平分线的交点,若∠BPC=72°,连接AP,则∠BAP=18 度. 分析 由∠BPC=72°,推出∠ECB+∠DBC=2(∠PCB+∠PBC)=216°,推出∠ACB+∠ABC=180°-∠ECB+180°-∠DBC=144°,根据∠BAC=180°-(∠ACB+∠ABC),即可求出∠BAC,再证明,PA平分∠DAE,由此即可解决问题.
解答 解:∵∠BPC=72°,
∴∠PCB+∠PBC=180°-∠BPC=108°,
∵∠ECB=2∠BCP,∠CBD=2∠PBC,
∴∠ECB+∠DBC=2(∠PCB+∠PBC)=216°,
∴∠ACB+∠ABC=180°-∠ECB+180°-∠DBC=144°,
∴∠BAC=180°-(∠ACB+∠ABC)=36°,
作PM⊥AE于M,PN⊥AD于N,PH⊥BC于H.
∵∠PCM=∠PCB,∠PBD=∠PBC,
∴PM=PH,PH=PN,
∴PM=PN,
∴∠PAB=∠PAE,
∴∠BAP=$\frac{1}{2}$∠BAC=18°,
故答案为18.
点评 本题考查三角形的外角平分线、角平分线性质定理和判定定理等知识,解题的关键是学会添加常用辅助线,掌握判定角平分线的方法,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com