
如图,为测量某塔AB的高度,在离塔底部10米处目测其塔顶A,仰角为60°,目高1.5米,则求该塔的高度为 米.(参考数据: ≈1.41,
≈1.41,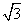 ≈1.73)
≈1.73)


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
如图,矩形ABCD中,AB=2,BC=1,O是AB的中点,动点P从B点开始沿着边BC,CD运动到点D结束.设BP=x,OP=y,则y关于x的函数图象大致为( )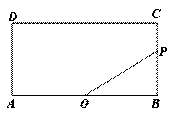
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线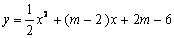 的对称轴为直线x=1,与x轴交于A,B 两点(点A在点B的左侧),与y轴交于点C.
的对称轴为直线x=1,与x轴交于A,B 两点(点A在点B的左侧),与y轴交于点C.
(1)求m的值;
(2)求A,B,C三点的坐标;
(3)过点C作直线 ∥x轴,将该抛物线在y轴左侧的部分沿直线
∥x轴,将该抛物线在y轴左侧的部分沿直线 翻折,抛物线的其余部分保持不变,得到一个新的图象,记为G.请你结合图象回答:
翻折,抛物线的其余部分保持不变,得到一个新的图象,记为G.请你结合图象回答:
当直线 与图象G只有一个公共点时,求b的取值范围.
与图象G只有一个公共点时,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知梯形ABCD,请使用无刻度直尺画图。
(1)在图1中画一个与梯形ABCD面积相等,且以CD为边的三角形;
(2)在图2中画一个与梯形ABCD面积相等,且以AB为边的平行四边形。

查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A、B重合),点F在BC边上(不与点B、C重合)。
第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;
第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;
依此操作下去…

(1)图2中的三角形EFD是经过两次操作后得到的,其形状为____,求此时线段EF的长;
(2)若经过三次操作可得到四边形EFGH。
①请判断四边形EFGH的形状为______,此时AE与BF的数量关系是______。
②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直角三角板 ABC 的斜边 AB=12cm,∠A=300,将三角板 ABC 绕 C 顺时针旋转 900至三角板 A/B/C/的位置后,再沿 CB 方向向左平移,使点 B/落在原三角板 ABC 的斜边 AB 上,则三角板 A/B/C/平移的距离为 ( )

(A)6 cm (B)4 cm (C)( )cm (D)(
)cm (D)( )cm
)cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com