
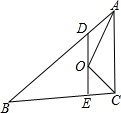
 如图,在△ABC中,AB=5cm,BC=3cm,∠BAC与∠BCA的平分线相交于点O,点D在AB上,且AD=OD.DO的延长线交BC于E.试求△BDE的周长.
如图,在△ABC中,AB=5cm,BC=3cm,∠BAC与∠BCA的平分线相交于点O,点D在AB上,且AD=OD.DO的延长线交BC于E.试求△BDE的周长. 分析 由AD=OD,得到∠DAO=∠DOA,根据角平分线的性质得到∠DOA=∠OAC,由平行线的判定得到DE∥AC,得到∠EOC=∠OCA,由等量代换得到角相等,根据等角对等边得到OE=CE,于是得到△BDE的周长=8.
解答 解:∵AD=OD,
∴∠DAO=∠DOA,
∵∠DAO=∠OAC,
∴∠DOA=∠OAC,
∴DE∥AC,
∴∠EOC=∠OCA,
∵∠OCA=∠OCE,
∴∠EOC=∠ECO,
∴OE=CE,
∴BE+DE+BD=BE+OE+OD+BD=BE+EC+BD+DA=AB+BC=5+3=8,
∴△BDE的周长=8.
点评 本题考查了角平分线的性质,平行线的性质,等腰三角形的判定与性质,三角形周长的求法,能通过等量代换得到相等的角是解题的关键.


科目:初中数学 来源: 题型:选择题
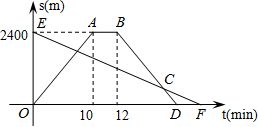 小明早8点从家骑自行车出发,沿一条直路去邮局办事,小明出发的同时,他的爸爸从邮局沿同一条道路步行回家,小明在邮局停留了一会后沿原路以原速度返回,小明比爸爸早3分钟到家.设他们与家的距离S(m)与离开家的时间t(min)之间函数关系的如图所示,有下列说法:①邮局与家的距离为2400米;②小明到家的时间为8:22分;③爸爸的速度为96mAmin;④小明在返回途中离家480米处于爸爸相遇,其中正确的说法有( )
小明早8点从家骑自行车出发,沿一条直路去邮局办事,小明出发的同时,他的爸爸从邮局沿同一条道路步行回家,小明在邮局停留了一会后沿原路以原速度返回,小明比爸爸早3分钟到家.设他们与家的距离S(m)与离开家的时间t(min)之间函数关系的如图所示,有下列说法:①邮局与家的距离为2400米;②小明到家的时间为8:22分;③爸爸的速度为96mAmin;④小明在返回途中离家480米处于爸爸相遇,其中正确的说法有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
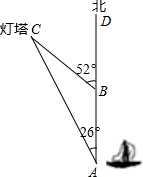 如图,上午10时,一艘船从A出发以20海里/时的速度向正北方向航行,11时45分到达B处,从A处测得灯塔C在北偏西26°方向,从B处测得灯塔C在北偏西52°方向,求B处到达塔C的距离.
如图,上午10时,一艘船从A出发以20海里/时的速度向正北方向航行,11时45分到达B处,从A处测得灯塔C在北偏西26°方向,从B处测得灯塔C在北偏西52°方向,求B处到达塔C的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
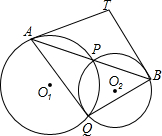 如图,⊙O1与⊙O2相交于P、Q两点,过P点作两圆的割线分别交于⊙O1与⊙O2于A、B,过A、B分别作两圆的切线相交于T,求证:T、A、Q、B四点共圆.
如图,⊙O1与⊙O2相交于P、Q两点,过P点作两圆的割线分别交于⊙O1与⊙O2于A、B,过A、B分别作两圆的切线相交于T,求证:T、A、Q、B四点共圆.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com