
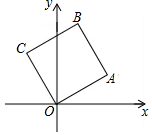
 如图,点A在第一象限内,其坐标为(2,1),以OA为边在x轴上方作正方形OABC,则正方形OABC的顶点C的坐标是( )
如图,点A在第一象限内,其坐标为(2,1),以OA为边在x轴上方作正方形OABC,则正方形OABC的顶点C的坐标是( )| A. | (-2,1) | B. | (1,3) | C. | (1,2) | D. | (-1.2) |
科目:初中数学 来源: 题型:解答题
 如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高(ycm)是指距(xcm)的一次函数.下表是测得的一组数据:
如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高(ycm)是指距(xcm)的一次函数.下表是测得的一组数据:| 指距x(cm) | 19 | 20 | 21 |
| 身高y(cm) | 151 | 160 | 169 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知双曲线y=$\frac{k}{x}$,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
如图,已知双曲线y=$\frac{k}{x}$,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
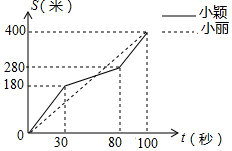 小丽和小颖进行400米耐力测试,他们同时起跑,同时到达终点,所跑的路程y(米)与所用时间t(秒)之间的关系如图所示,则他们第一次相遇的时间是起跑后第60秒.
小丽和小颖进行400米耐力测试,他们同时起跑,同时到达终点,所跑的路程y(米)与所用时间t(秒)之间的关系如图所示,则他们第一次相遇的时间是起跑后第60秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
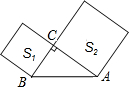 如图,以Rt△ABC的两直角边为边向外作正方形,其面积分别为S1、S2,若S1=9,S2=16,则斜边AB的长是( )
如图,以Rt△ABC的两直角边为边向外作正方形,其面积分别为S1、S2,若S1=9,S2=16,则斜边AB的长是( )| A. | 3 | B. | 4 | C. | 5 | D. | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com