练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．用一个平面截一个几何体，所得的截面是圆，请你写出一种几何体球，圆柱，圆锥等．

    分析 球体的截面永远是圆，横截圆柱和圆锥（截面平行于底面时）也可使截面为圆．

    解答 解：球体的截面永远是圆，横截圆柱和圆锥（截面平行于底面时）也可使截面为圆，因此，用一个平面截一个几何体，得出的截面是圆，那么，这个几何体可能是球，圆柱，圆锥等．
    故答案为：球，圆柱，圆锥等．

    点评 此题考查了截一个几何体，截面的形状既与被截的几何体有关，还与截面的角度和方向有关．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

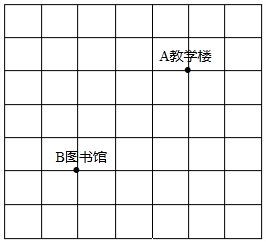    2．2016年8月31日，东明一中新校区启用，学校迎来高一新生，为了保证新生顺利入学．学校在校园内设立了团员“迎接接待站”，并向家长和学生提供“学校建筑分布图，协助新生完成报到流程，尽全力提供周到的服务，如图为分布图的一部分，方格纸中每个小方格都是边长为1个单位的正方形，若教学楼的坐标为A（1，2），图书馆的位置坐标为B（-2，-1），解答以下问题：
    （1）在图中找到坐标系中的原点，并建立直角坐标系；
    （2）若体育馆的坐标为C（1，-3），食堂坐标为D（2，0），请在图中标出体育馆和食堂的位置；
    （3）顺次连接教学楼、图书馆、体育馆、食堂得到四边形ABCD，求四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

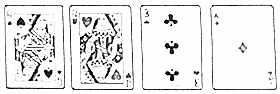    3．从一幅扑克牌（去掉大、小王）中任意抽取4张，根据牌面上的数字进行混合运算（每张牌只能用一次），使得运算结果为24或-24，其中红色扑克代表负数，黑色扑克代表正数，J、Q、K分别代表11，12，13．如果抽到的是下列四张扑克（一张黑Q，一张红Q，一张黑3，一张红A）凑成24所列的算式是12×3-（-12）×（-1）
    提示：【可运用加、减、乘、除、乘方（例如数2，6，可列62=36或26=64）运算，可用括号：注意：例如4×（1+2+3）=24与（2+1+3）×4=24只是顺序不同，属同一个算式】

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．若点A（a-2，3）和点B（-1，b+5）关于y轴对称，则点C（a，b）在第四象限．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．我们经常做一种“石头、剪刀、布”游戏，小亮与小明也一起玩这种游戏，两同学同时出“剪刀”的概率是$\frac{1}{9}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列各数是无理数的是（　　）
    A．3.14B．-$\sqrt{9}$C．πD．$\frac{22}{7}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．阅读材料：黑白双雄，纵横江湖，双剑合璧，天下无敌，这是武侠小说中的常见描述，其意指两个人合在一起，取长补短，威力无比．在二次根式中也有这样相辅相成的例子．
    如（2+$\sqrt{3}$）（2-$\sqrt{3}$）=22-（-$\sqrt{3}$）2=1，（$\sqrt{5}$+$\sqrt{2}$）（$\sqrt{5}$-$\sqrt{2}$）=（$\sqrt{5}$）2-（$\sqrt{2}$）2=3，它们的积是有理数，我们说这两个二次根式互为有理化因式，其中一个是另一个的有理数因素．于是，我们可以将下面的式子化简：
    $\frac{1}{2-\sqrt{3}}$=$\frac{2+\sqrt{3}}{（2-\sqrt{3}）（2+\sqrt{3}）}$=2+$\sqrt{3}$
    解决问题：
    （1）4+$\sqrt{7}$的一个有理化因式是4-$\sqrt{7}$．
    （2）计算：$\frac{1}{\sqrt{3}+1}$+$\frac{1}{\sqrt{5}+\sqrt{3}}$+$\frac{1}{\sqrt{7}+\sqrt{5}}$+…+$\frac{1}{\sqrt{2017}+\sqrt{2015}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列属于同类项的是（　　）
    A．$\frac{x}{2}$与$\frac{1}{x}$B．-m3与n3C．$\frac{2}{3}$a2b与2ab2D．22与32

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

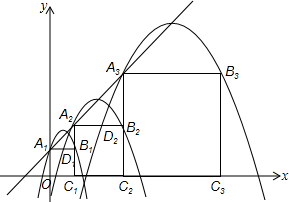    2．在平面直角坐标系xOy中，正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…，按如图的方式放置．点A1，A2，A3，…，An和点C1，C2，C3，…，Cn分别落在直线y=x+1和x轴上．抛物线L1过点A1，B1，且顶点在直线y=x+1上，抛物线L2过点A2，B2，且顶点在直线y=x+1上，…，按此规律，抛物线Ln过点An，Bn，且顶点也在直线y=x+1上，其中抛物线L2交正方形A1B1C1O的边A1B1于点D1，抛物线L3交正方形A2B2C2C1的边A2B2于点D2，…，抛物线Ln+1交正方形AnBnCnCn-1的边AnBn于点Dn（其中n≥2且n为正整数）．
    （1）直接写出下列点的坐标：B1（1，1），B2（3，2），B3（7，4）；
    （2）写出抛物线L2、L3的解析式，并写出其中一个解析式求解过程，再猜想抛物线Ln的顶点坐标
    （3）设A1D1=k1•D1B1，A2D2=k2•D2B2，试判断k1与k2的数量关系并说明理由．

    查看答案和解析>>

    同步练习册答案