
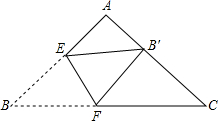
 将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B',折痕为EF.已知AB=AC=2,cosC=
将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B',折痕为EF.已知AB=AC=2,cosC=| 3 | 4 |
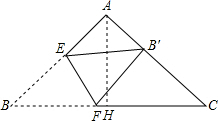 解:作AH⊥BC,垂足为H,在Rt△ACH中,CH=AC•cosC=
解:作AH⊥BC,垂足为H,在Rt△ACH中,CH=AC•cosC=| 3 |
| 2 |
| B′E |
| BC |
| AB′ |
| AC |
| x |
| 3 |
| 2-x |
| 2 |
| 6 |
| 5 |
| 6 |
| 5 |


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:
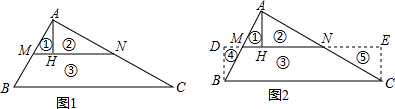
.将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片,如图(1);再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE、DF,如图(2),证明:四边形AEDF是菱形.
 |
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(广西钦州) 题型:解答题
(本题满分9分)将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片,如图(1);再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE、DF,如图2,证明:四边形AEDF是菱形.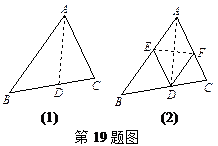
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(广西钦州) 题型:解答题
(本题满分9分)将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片,如图(1);再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE、DF,如图2,证明:四边形AEDF是菱形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com