
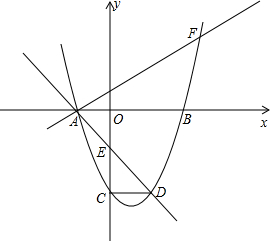
 ��ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬������y=ax2+bx-5��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ��ΪC��ֱ��y=-x-2������A�����������ڵ�D����y���ڵ�E������CD�����ҡ�ADC=45�㣮
��ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬������y=ax2+bx-5��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ��ΪC��ֱ��y=-x-2������A�����������ڵ�D����y���ڵ�E������CD�����ҡ�ADC=45�㣮���� ��1����ȷ��C��0��-5����A��-2��0����E��0��-2��������жϡ�OAEΪ����ֱ�������Σ����ԡ�OAE=45�㣬���ǿ��ж�CD��x�ᣬ���ԡ�CDEΪ����ֱ�������Σ���D��3��-5����Ȼ�����ô���ϵ�����������ߵĽ���ʽ��
��2��ֱ��AF��y����G����ͼ���������Ǻ����õ�s$\frac{OG}{AG}$=$\frac{1}{\sqrt{5}}$����OG=t����AG=$\sqrt{5}$t��OA=2t������2t=2�����t=1�����ǵõ�G��0��1������ֱ��AG�Ľ���ʽΪy=$\frac{1}{2}$x+1��Ȼ��ͨ���ⷽ����$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{y=\frac{1}{2}{x}^{2}-\frac{3}{2}x-5}\end{array}\right.$��F������ꣻ
��3����EM��PQ��M����ͼ��������ֱ�ߴ�ֱ���⣬��PQ�Ľ���ʽΪy=-2x+m��������ֱ��ƽ������õ�EM�Ľ���ʽΪy=$\frac{1}{2}$x-2����ⷽ����$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{y=-2x+m}\end{array}\right.$��Q��$\frac{2}{5}$m-$\frac{2}{5}$��$\frac{1}{5}$m+$\frac{4}{5}$������P��a��b�������ݵ��������ε����ʵ�M���߶�PQ���е㣬�����߶��е����깫ʽ�õ�M�������Ϊ[$\frac{1}{2}$��a+$\frac{2}{5}$m-$\frac{2}{5}$����$\frac{1}{2}$��b+$\frac{1}{5}$m+$\frac{4}{5}$��]�����õ�M����ֱ��y=$\frac{1}{2}$x-2�ϵ�$\frac{1}{4}$��a+$\frac{2}{5}$m-$\frac{2}{5}$��-2=$\frac{1}{2}$��b+$\frac{1}{5}$m+$\frac{4}{5}$��������b=$\frac{1}{2}$a-5��Ȼ���P��a��$\frac{1}{2}$a-5�����������߽���ʽ��$\frac{1}{2}$a2-$\frac{3}{2}$a-5=$\frac{1}{2}$a-5���������a�ķ��̼��ɵõ�P�����꣮
��� �⣺��1����x=0ʱ��y=ax2+bx-5=-5����C��0��-5����
��y=0ʱ��-x-2=0�����x=-2����A��-2��0����
��x=0ʱ��y=-x-2=0����E��0��-2����
��OA=OE��
���OAEΪ����ֱ�������Σ�
���OAE=45�㣬
�ߡ�ADC=45�㣬
��CD��x�ᣬ
���CDEΪ����ֱ�������Σ�
��CD=CE=3��
��D��3��-5����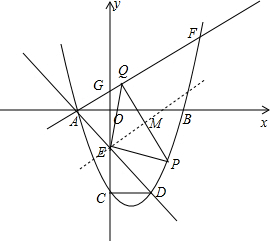
��A��-2��0����D��3��-5������y=ax2+bx-5��$\left\{\begin{array}{l}{4a-2b-5=0}\\{9a+3b-5=-5}\end{array}\right.$�����$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{3}{2}}\end{array}\right.$��
�������ߵĽ���ʽΪy=$\frac{1}{2}$x2-$\frac{3}{2}$x-5��
��2��ֱ��AF��y����G����ͼ��
��Rt��AOG��sin��OAG=$\frac{OG}{AG}$=$\frac{\sqrt{5}}{5}$=$\frac{1}{\sqrt{5}}$��
��OG=t��AG=$\sqrt{5}$t��
��OA=$\sqrt{��\sqrt{5}t��^{2}+{t}^{2}}$=2t��
��2t=2�����t=1��
��G��0��1����
��ֱ��AG�Ľ���ʽΪy=$\frac{1}{2}$x+1��
�ⷽ����$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{y=\frac{1}{2}{x}^{2}-\frac{3}{2}x-5}\end{array}\right.$��$\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=6}\\{y=4}\end{array}\right.$��
��F���������6��4����
��3����EM��PQ��M����ͼ��
��PQ��AF��
��PQ�Ľ���ʽ����Ϊy=-2x+m��
��EM��AF��
��EM�Ľ���ʽΪy=$\frac{1}{2}$x-2��
�ⷽ����$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{y=-2x+m}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{2}{5}m-\frac{2}{5}}\\{y=\frac{1}{5}m+\frac{4}{5}}\end{array}\right.$����Q��$\frac{2}{5}$m-$\frac{2}{5}$��$\frac{1}{5}$m+$\frac{4}{5}$����
��P��a��b����
��EQ=EP��
��QM=PM��
��M�������Ϊ[$\frac{1}{2}$��a+$\frac{2}{5}$m-$\frac{2}{5}$����$\frac{1}{2}$��b+$\frac{1}{5}$m+$\frac{4}{5}$��]��
��M[$\frac{1}{2}$��a+$\frac{2}{5}$m-$\frac{2}{5}$����$\frac{1}{2}$��b+$\frac{1}{5}$m+$\frac{4}{5}$��]����y=$\frac{1}{2}$x-2��$\frac{1}{4}$��a+$\frac{2}{5}$m-$\frac{2}{5}$��-2=$\frac{1}{2}$��b+$\frac{1}{5}$m+$\frac{4}{5}$����
��b=$\frac{1}{2}$a-5��
��P��a��$\frac{1}{2}$a-5����
��P��a��$\frac{1}{2}$a-5������y=$\frac{1}{2}$x2-$\frac{3}{2}$x-5��$\frac{1}{2}$a2-$\frac{3}{2}$a-5=$\frac{1}{2}$a-5�����a1=0��a2=4��
��P��������0��-5����4��-3����
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ���������������κ��������ʺ͵���ֱ�������εĹ�ϵ�������ô���ϵ������������ʽ����������һ�κ���ͼ��ƽ�л�ֱ��һ����ϵ���Ĺ�ϵ������������ͼ�����ʣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-x+2y����x-2y�� | B�� | ��2x-y����2y+x�� | C�� | ��m-n����n-m�� | D�� | 99��101 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
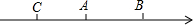 ��ͼ��������A��B�����ʾ�����ֱ�Ϊ-1��$\sqrt{3}$����A��BC���е㣬���C����ʾ������������
��ͼ��������A��B�����ʾ�����ֱ�Ϊ-1��$\sqrt{3}$����A��BC���е㣬���C����ʾ������������| A�� | -2-$\sqrt{3}$ | B�� | -1-$\sqrt{3}$ | C�� | -2+$\sqrt{3}$ | D�� | 1+$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
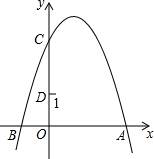 ��ͼ��������y=-x2+2x+3��y�ύ�ڵ�C����D��0��1������P���������ϵĶ��㣬����PCD����CDΪ�ĵ��������Σ����P������Ϊ��1+$\sqrt{2}$��2����1-$\sqrt{2}$��2����
��ͼ��������y=-x2+2x+3��y�ύ�ڵ�C����D��0��1������P���������ϵĶ��㣬����PCD����CDΪ�ĵ��������Σ����P������Ϊ��1+$\sqrt{2}$��2����1-$\sqrt{2}$��2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
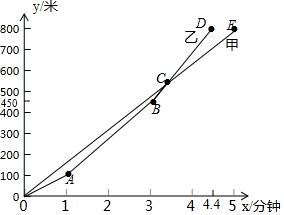 �������ɣ�������Ϊ�����ʫ����ԭ��ij�о������������ס�����֧���۶��ڱ���ʱ��·��y���ף���ʱ��x�����ӣ�֮��ĺ���ͼ����ͼ��ʾ������ͼ��ش��������⣺
�������ɣ�������Ϊ�����ʫ����ԭ��ij�о������������ס�����֧���۶��ڱ���ʱ��·��y���ף���ʱ��x�����ӣ�֮��ĺ���ͼ����ͼ��ʾ������ͼ��ش��������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
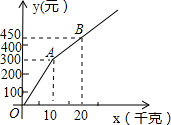 �ס�������ӣ�Ҳ�ժ��Ʒ����ͬ�����ۼ۸�Ҳ��ͬ������һ�ڼ䡱�����Ҿ��Ƴ����Żݷ������ײ�ժ���Żݷ����ǣ��οͽ��蹺��50Ԫ����Ʊ����ժ�IJ�ݮ�����Żݣ��Ҳ�ժ���Żݷ����ǣ��οͽ����蹺����Ʊ����ժ�IJ�ݮ����һ�������������ִ����Żݣ��Ż��ڼ䣬��ij�ο͵IJ�ݮ��ժ��Ϊx��ǧ�ˣ����ڼײ�ժ�����ܷ���Ϊy1��Ԫ�������Ҳ�ժ�����ܷ���Ϊy2��Ԫ����ͼ������OAB��ʾy2��x֮��ĺ�����ϵ��
�ס�������ӣ�Ҳ�ժ��Ʒ����ͬ�����ۼ۸�Ҳ��ͬ������һ�ڼ䡱�����Ҿ��Ƴ����Żݷ������ײ�ժ���Żݷ����ǣ��οͽ��蹺��50Ԫ����Ʊ����ժ�IJ�ݮ�����Żݣ��Ҳ�ժ���Żݷ����ǣ��οͽ����蹺����Ʊ����ժ�IJ�ݮ����һ�������������ִ����Żݣ��Ż��ڼ䣬��ij�ο͵IJ�ݮ��ժ��Ϊx��ǧ�ˣ����ڼײ�ժ�����ܷ���Ϊy1��Ԫ�������Ҳ�ժ�����ܷ���Ϊy2��Ԫ����ͼ������OAB��ʾy2��x֮��ĺ�����ϵ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com