练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    甲、乙、丙三位同学打乒乓球，想通过“手心手背”游戏来决定其中哪两人先打．规则如下：三人同时各用一只手随机出示手心或手背，若只有两人手势相同(都是手心或都是手背)，则这两人先打；若三人手势相同，则重新决定．那么通过一次“手心手背”游戏能决定甲打乒乓球的概率是_________．

    【解析】试题解析：分别用A、a表示手心和手背， 画树状图为： 共有8种等可能的结果数，其中甲打乒乓球的结果数为4， 所以通过一次“手心手背”游戏能决定甲打乒乓球的概率=． 故答案为： .
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版九年级年级数学下册第二十九章 达标检测卷 题型：填空题

    如图所示，电视台的摄像机1、2、3、4在不同位置拍摄了四幅画面，则：

    A图象是_____号摄像机所拍，

    B图象是_____号摄像机所拍，

    C图象是_____号摄像机所拍，

    D图象是_____号摄像机所拍．

    2 3 4 1 【解析】如果以3号机为正面，那么3号机拍的是主视图，4号机拍的是左视图，2号机拍的是右视图，1号机拍的是后视图， 所以A图象是2号机拍的，B图象是3号机拍的，C图象是4号机拍的，D图象是1号机拍的. 故答案为： 2 ， 3 ， 4 ， 1.

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级下册数学第五章相交线与平行线单元检测卷 题型：解答题

    如图，直线a、b被直线l所截，已知∠1=40°，试求∠2的同位角及同旁内角的度数．

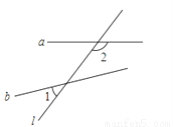
    ∠2的同位角是140°，∠2的同旁内角是40°． 【解析】试题分析： 首先要确定∠2的同位角、同旁内角是哪一个：因l为截线，这两个角与∠2必然位于l的同旁，即直线l的右边的∠3与∠4；再根据对顶角性质及补角定理，就可求出两角大小. 【解析】 如图， ∵∠1=40°， ∴∠4=∠1=40°，∠3=180°﹣∠1=140°， 即∠2的同位角是140°，∠2的同旁内...

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级下册数学第五章相交线与平行线单元检测卷 题型：单选题

    如图，已知直线a、b被直线c所截，那么∠1的同位角是（ ）

    A. ∠2 B. ∠3 C. ∠4 D. ∠5

    D 【解析】【解析】 ∠1的同位角是∠5， 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型：解答题

    如图，有两部不同型号的手机(分别记为A，B)和与之匹配的2个保护盖(分别记为a，b)散乱地放在桌子上．

    (1)若从手机中随机取一部，再从保护盖中随机取一个，求恰好匹配的概率；

    (2)若从手机和保护盖中随机取两个，用画树状图法或列表法求恰好匹配的概率．

    （1）（2） 【解析】试题分析：（1）由题意可得有Aa，Ab，Ba，Bb四种情况．恰好匹配的有Aa，Bb两种情况，然后直接利用概率公式求解即可求得答案； （2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果以及恰好匹配的情况，再利用概率公式即可求得答案． 试题解析：(1)从手机中随机抽取一个，再从保护盖中随机取一个，有Aa，Ab，Ba，Bb四种结果，每种结果出现的可能性...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型：填空题

    一个不透明的口袋里有10个黑球和若干个黄球，从口袋中随机摸出一球记下其颜色，再把它放回口袋中摇匀，重复上述过程，共试验200次，其中有120次摸到黄球，由此估计袋中的黄球有________个．

    15 【解析】试题分析：黄球的概率近似为=，设袋中有x个黄球，则=，解得x=15．故答案为：15．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型：单选题

    一次掷两枚质地均匀的硬币，出现两枚硬币都正面朝上的概率是（ ）

    A. B. C. D.

    D 【解析】试题分析：先利用列表法与树状图法表示所有等可能的结果n，然后找出某事件出现的结果数m，最后计算概率．同时掷两枚质地均匀的硬币一次，共有正正、反反、正反、反正四种等可能的结果，两枚硬币都是正面朝上的占一种，所以两枚硬币都是正面朝上的概率=1÷4=．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学人教版上册 全册综合测试卷 题型：填空题

    如图所示， AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3=_____.

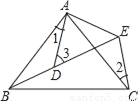
    55° 【解析】求出∠BAD=∠EAC，证△BAD≌△EAC，推出∠2=∠ABD=30°，根据三角形的外角性质求出即可． 【解析】 ∵∠BAC=∠DAE， ∴∠BAC﹣∠DAC=∠DAE﹣∠DAC， ∴∠1=∠EAC， 在△BAD和△EAC中， AB=AC，∠BAD=∠EAC， ∴△BAD≌△EAC（SAS）， ∴∠2=∠ABD=30°， ∵...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十七章达标检测卷 题型：解答题

    如图，要在木里县某林场东西方向的两地之间修一条公路MN，已知点C周围200 m范围内为原始森林保护区，在MN上的点A处测得C在A的北偏东45°方向上，从A向东走600 m到达B处，测得C在点B的北偏西60°方向上.

    （1）MN是否穿过原始森林保护区?为什么?(参考数据: 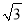≈1.732)

    （2）若修路工程顺利进行，要使修路工程比原计划提前5天完成，需将原定的工作效率提高25%，则原计划完成这项工程需要多少天?

    （1）MN不会穿过原始森林保护区，理由见解析；（2）原计划完成这项工程需要25天. 【解析】试题分析：（1）要求MN是否穿过原始森林保护区，也就是求C到MN的距离．要构造直角三角形，再解直角三角形； （2）根据题意列方程求解． 试题解析：（1）如图，过C作CH⊥AB于H， 设CH=x，由已知有∠EAC=45°, ∠FBC=60° 则∠CAH=45°, ∠CBA=30°...

    查看答案和解析>>

    同步练习册答案