
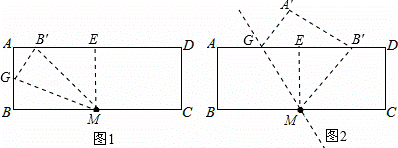
如图是长为40cm,宽为16cm的矩形纸片,M点为一边上的中点,沿过M的直线翻折.若中点M所在边的一个顶点不能落在对边上,那么折痕长度为 cm.

10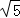 或8
或8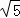
解:分两种情况考虑:
(i)如图1所示,过M作ME⊥AD于E,G在AB上,B′落在AE上,可得四边形ABME为矩形,
∴EM=AB=16,AE=BM,
又∵BC=40,M为BC的中点,
∴由折叠可得:B′M=BM=B C=20,
C=20,
在Rt△EFB′中,根据勾股定理得:B′E=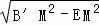 =12,
=12,
∴AB′=AE﹣B′E=20﹣12=8,
设AG=x,则有GB′=GB=16﹣x,
在Rt△AGB′中,根据勾股定 理得:GB′2=AG2+AB′2,
理得:GB′2=AG2+AB′2,
即(16﹣x)2=x2+82,
解得:x=6,
∴GB=16﹣6=10,
在Rt△GBF中,根据勾股定理得:GM=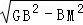 =10
=10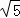 ;
;
(ii)如图2所示,过F作FE⊥AD于E,G在AE上,B′落在ED上,可得四边形ABME为矩形,
∴EM=AB=16,AE=BM,
又BC=40,M为BC的中点,
∴由折叠可得:B′M=BM=BC=20,
在Rt△EMB′中,根据勾股定理得:B′E=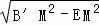 =12,
=12,
∴AB′=AE﹣B′E=20﹣12=8,
设AG=A′G=y,则GB′=AB′﹣AG=AE+EB′﹣AG=32﹣y,A′B′=AB=16,
在Rt△A′B′G中,根据勾股定理得:A′G2+A′B′2=GB′2,
即y2+162=(32﹣y)2,
解得:y=12,
∴AG=12,
∴GE=AE﹣AG=20﹣12=8,
在Rt△GEF中,根据勾股定理得:GM=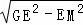 =8
=8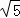 ,
,
综上,折痕FG=10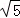 或8
或8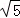 .
.
故答案为:10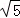 或8
或8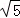 .
.


科目:初中数学 来源: 题型:
如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.
(1)求证:△ABC∽△BCD;
(2)求x的值;
(3)求cos36°﹣cos72°的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,直线l与x轴相交于点M,与y轴相交于点N,Rt△MON的外心为点A(,﹣2),反比例函数y=(x>0)的图象过点A.
(1)求直线l的解析式;
(2)在函数y=(x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com