
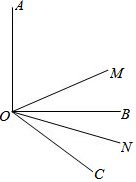
 (1)如图,已知∠AOB=90°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.求∠MON的度数.
(1)如图,已知∠AOB=90°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.求∠MON的度数.分析 (1)根据角平分线的定义得到∠MOC=$\frac{1}{2}$∠AOC,∠NOC=$\frac{1}{2}$∠BOC,则∠MON=∠MOC-∠NOC=$\frac{1}{2}$(∠AOC-∠BOC)=$\frac{1}{2}$∠AOB,然后把∠AOB的度数代入计算即可;
(2)根据角平分线的定义得到∠MOC=$\frac{1}{2}$∠AOC,∠NOC=$\frac{1}{2}$∠BOC,则∠MON=∠MOC-∠NOC=$\frac{1}{2}$(∠AOC-∠BOC)=$\frac{1}{2}$∠AOB,然后把∠AOB的度数代入计算即可;
(3)先得到∠AOC=90°+β,再根据角平分线的定义得到∠COM=$\frac{1}{2}$∠AOC=$\frac{1}{2}$(90°+β),∠CON=$\frac{1}{2}$∠BOC=$\frac{1}{2}$β,然后利用∠MON=∠COM-∠CON进行计算;
(4)利用前面计算的结论得到∠MON=$\frac{1}{2}$∠AOB.
解答 解:(1)∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=$\frac{1}{2}$∠AOC,∠NOC=$\frac{1}{2}$∠BOC,
∵∠AOC=∠AOB+∠BOC,
∴∠MON=∠MOC-∠NOC=$\frac{1}{2}$(∠AOB+∠BOC-∠BOC)=$\frac{1}{2}$∠AOB,
∵∠AOB=90°,
∴∠MON=$\frac{1}{2}$×90°=45°;
(2))∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=$\frac{1}{2}$∠AOC,∠NOC=$\frac{1}{2}$∠BOC,
∵∠AOC=∠AOB+∠BOC,
∴∠MON=∠MOC-∠NOC=$\frac{1}{2}$(∠AOB+∠BOC-∠BOC)=$\frac{1}{2}$∠AOB,
∵∠AOB=α,
∴∠MON=$\frac{1}{2}$×α=$\frac{α}{2}$;
(3)∵∠AOB=90°,∠BOC=β,
∴∠AOC=90°+β,
∵OM平分∠AOC,ON平分∠BOC,
∴∠COM=$\frac{1}{2}$∠AOC=$\frac{1}{2}$(90°+β),∠CON=$\frac{1}{2}$∠BOC=$\frac{1}{2}$β,
∴∠MON=∠COM-∠CON=$\frac{1}{2}$(90°+β)-$\frac{1}{2}$β=45°;
(4)从(1)(2)(3)的结果中可以看出∠MON=$\frac{1}{2}$∠AOB,而与∠BOC的大小无关.
点评 本题考查了角的计算:利用几何图形计算几个角的和或差.也考查了角平分线的定义.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
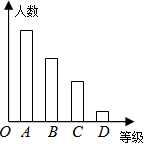 某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级.现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题:
某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级.现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
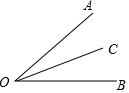 如图,OC为∠AOB内一条射线,下列条件中能确定OC平分∠AOB的是( )
如图,OC为∠AOB内一条射线,下列条件中能确定OC平分∠AOB的是( )| A. | ∠BOC=$\frac{1}{2}$∠AOC | B. | ∠AOC+∠COB=∠AOB | C. | ∠AOB=2∠AOC | D. | ∠COB=∠AOB-∠AOC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
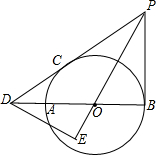 如图,AB为⊙O的直径,PB、PC分别是⊙O的切线,切点为B、C,PC、BA的延长线交于点D,DE⊥PO,交PO的延长线于点E.
如图,AB为⊙O的直径,PB、PC分别是⊙O的切线,切点为B、C,PC、BA的延长线交于点D,DE⊥PO,交PO的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com