
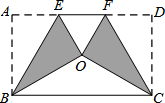
 将矩形纸片ABCD按如图方式折叠,BE、CF为折痕,折叠后点A和点D都落在点O处,若△EOF是等边三角形,则$\frac{AB}{AD}$的值为$\frac{\sqrt{3}}{3}$.
将矩形纸片ABCD按如图方式折叠,BE、CF为折痕,折叠后点A和点D都落在点O处,若△EOF是等边三角形,则$\frac{AB}{AD}$的值为$\frac{\sqrt{3}}{3}$. 分析 由△EOF是等边三角形,可得EF=OE=OF,∠OEF=60°,又由由折叠的性质可得:OE=AE,OF=DF,∠AEB=∠OEB,则可得AD=3AE,∠AEB=60°,则可证得AB=$\sqrt{3}$AE,继而求得答案.
解答 解:∵△EOF是等边三角形,
∴EF=OE=OF,∠OEF=60°,
由折叠的性质可得:OE=AE,OF=DF,∠AEB=∠OEB,
∴AD=3AE,∠AEB=$\frac{180°-∠OEF}{2}$=60°,
∵四边形ABCD是矩形,
∴∠A=90°,
∴tan∠AEB=$\frac{AB}{AE}$=$\sqrt{3}$,
∴AB=$\sqrt{3}$AE,
∴$\frac{AB}{AD}$=$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{\sqrt{3}}{3}$.
点评 此题考查了折叠的性质、等边三角形的性质、矩形的性质以及三角函数等知识.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,C是⊙O上一点,∠ACD=∠B,AD⊥CD.
如图,AB是⊙O的直径,C是⊙O上一点,∠ACD=∠B,AD⊥CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
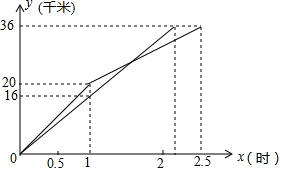 一次国际龙舟拉力赛中,上午9时,参赛龙舟同时出发,其中甲、乙两队在比赛时,路程y(千米)与时间x(小时)的函数关系如图所示,甲队在上午11时30分到达终点.
一次国际龙舟拉力赛中,上午9时,参赛龙舟同时出发,其中甲、乙两队在比赛时,路程y(千米)与时间x(小时)的函数关系如图所示,甲队在上午11时30分到达终点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
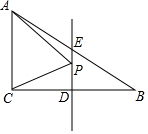 如图,△ABC中,∠ACB=90°,∠B=30°,AC=4cm,P为BC边的垂直平分线DE上一个动点,则△ACP的周长最小值为12cm.
如图,△ABC中,∠ACB=90°,∠B=30°,AC=4cm,P为BC边的垂直平分线DE上一个动点,则△ACP的周长最小值为12cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,OC是∠AOB内部的一条射线,且OM,ON分别平分∠AOC与∠BOC.
如图,OC是∠AOB内部的一条射线,且OM,ON分别平分∠AOC与∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com