
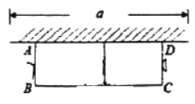
【题目】如图,有长为![]() 的篱笆,现一面利用墙(墙的最大可用长度
的篱笆,现一面利用墙(墙的最大可用长度![]() 为
为![]() )围成中间隔有一道篱笆的长方形花圃,设花圃的宽
)围成中间隔有一道篱笆的长方形花圃,设花圃的宽![]() 为
为![]() ,面积为
,面积为![]() .
.
(1)求![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)要围成面积为![]() 的花圃,
的花圃,![]() 的长是多少米?
的长是多少米?
【答案】(1)s=3x2+30x(![]() ≤x<10)(2)8米
≤x<10)(2)8米
【解析】
(1)设花圃的宽AB为xm,面积为Sm2,则BC的长为(303x)米,利用矩形的面积公式即可得出S与x的函数关系式,由x>0,0<303x≤20可得出x的取值范围;
(2)代入S=48可得出关于x的一元二次方程,解之即可得出x的值,结合(1)可确定x的值,此题得解.
(1)设花圃的宽AB为xm,面积为Sm2,则BC的长为(303x)米,
∴S=(303x)x=3x2+30x,
∵![]() ,
,
∴![]() ≤x<10.
≤x<10.
∴S与x的函数关系式为s=3x2+30x(![]() ≤x<10).
≤x<10).
(2)如果要围成面积为48m2的花圃,即当S=48时,48=3x2+30x,
则x210x+16=0,
解得:x1=2,x2=8.
∵![]() ≤x<10,
≤x<10,
∴x=8.
答:要围成面积为48m2的花圃,AB的长是8米.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
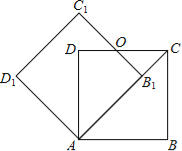
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与应用
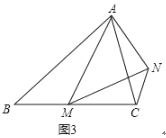
(提出问题)
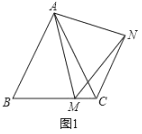
(1)如图1,在等边![]() 中,点
中,点![]() 是
是![]() 上的任意一点(不含端点
上的任意一点(不含端点![]() 、
、![]() ),连结
),连结![]() ,以
,以![]() 为边作等边
为边作等边![]() ,连结
,连结![]() .求证:
.求证:![]() .
.
(类比探究)
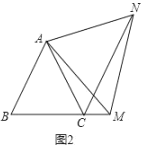
(2)如图2,在等边![]() 中,点
中,点![]() 是
是![]() 延长线上的任意一点(不含端点
延长线上的任意一点(不含端点![]() ),其它条件不变,(1)中结论
),其它条件不变,(1)中结论![]() 还成立吗?请说明理由.
还成立吗?请说明理由.
(拓展延伸)
(3)如图3,在等腰![]() 中,
中,![]() ,点
,点![]() 是
是![]() 上的任意一点(不含端点
上的任意一点(不含端点![]() 、
、![]() )连结
)连结![]() ,以
,以![]() 为边作等腰
为边作等腰![]() ,使顶角
,使顶角![]() .连结
.连结![]() .试探究
.试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边)
的左边)![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,点
,点![]() 为抛物线的顶点.
为抛物线的顶点.
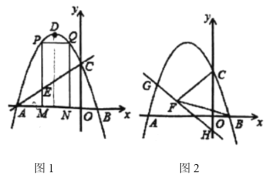
(1)求抛物线的解析式;
(2)点![]() 为线段
为线段![]() 上一点(点
上一点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,与直线
轴的垂线,与直线![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() ,过点
,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,可得矩形
,可得矩形![]() ,如图1,点
,如图1,点![]() 在点
在点![]() 左边,当矩形
左边,当矩形![]() 的周长最大时,求
的周长最大时,求![]() 的值,并求出此时的
的值,并求出此时的![]() 的面积;
的面积;
(3)已知![]() ,点
,点![]() 在抛物线上,连
在抛物线上,连![]() ,直线
,直线![]() ,垂足为
,垂足为![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人利用扑克牌玩“10点”游戏,游戏规则如下:
①将牌面数字作为“点数”,如红桃6的“点数”就是6(牌面点数与牌的花色无关);
②两人摸牌结束时,将所得牌的“点数”相加,若“点数”之和小于或等于10,此时“点数”之和就是“最终点数”,若“点数”之和大于10,则“最终点数”是0;
③游戏结束之前双方均不知道对方“点数”;
④判定游戏结果的依据是:“最终点数”大的一方获胜,“最终点数”相等时不分胜负.
现甲、乙均各自摸了两张牌,数字之和都是5,这时桌上还有四张背面朝上的扑克牌,牌面数字分别是4,5,6,7.

(1)若甲从桌上继续摸一张扑克牌,乙不再摸牌,则甲获胜的概率为 ;
(2)若甲先从桌上继续摸一张扑克牌,接着乙从剩下的扑克牌中摸出一张牌,然后双方不再摸牌,请用树状图或表格表示出这次摸牌后所有可能的结果,再列表呈现甲、乙的“最终点数”,并求乙获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
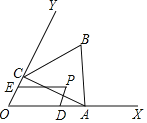
【题目】如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
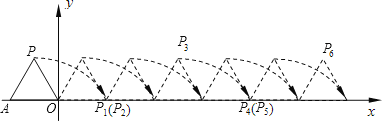
【题目】如图,将边长为1的正三角形OAP沿χ轴方向连续翻转若干次,点P依次落在点P1,P2,P3,…,P2018的位置,则点P2018的横坐标为( )
A.2016B.2017C.2018D.2019
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com