
商店上月收入为 元,本月的收入比上月的3倍少5元,本月的收入为__________元.(用含
元,本月的收入比上月的3倍少5元,本月的收入为__________元.(用含 的式子表示)
的式子表示)
科目:初中数学 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期检测八年级数学试卷 题型:单选题
若x+m与2-x的乘积中不含x的一次项,则实数m的值为( )
A. -2 B. 2 C. 0 D. 1
B 【解析】根据题意得: (x+m)(2?x)=2x?x2+2m?mx, ∵x+m与2?x的乘积中不含x的一次项, ∴m=2; 故选B.查看答案和解析>>
科目:初中数学 来源:云南民族大学附属中学2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
如图,将图中的平行四边形ABCD先绕D按顺时针方向旋转 后,再平移,使点D平移至E点,作出旋转及平移后的图形
后,再平移,使点D平移至E点,作出旋转及平移后的图形 保留作图痕迹
保留作图痕迹

查看答案和解析>>
科目:初中数学 来源:贵州省遵义市桐梓县2016-2017学年七年级上学期期末考试数学试卷 题型:解答题
如图,已知数轴上点B表示的为-5,点A是数轴上一点,且AB=12,动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,动点H从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为 (
( )秒.
)秒.
(1)写出数轴上点A表示的数 ;
(2)当动点P,H同时从点A和点B出发,运动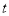 秒时,点P表示的数 ;点H表示的数 ;(用含
秒时,点P表示的数 ;点H表示的数 ;(用含 的代数式表示)
的代数式表示)
(3)动点P、H同时出发,问点H运动多少秒时追上点P?

查看答案和解析>>
科目:初中数学 来源:贵州省遵义市桐梓县2016-2017学年七年级上学期期末考试数学试卷 题型:解答题
计算题:
(1) 14﹣(﹣12 )+(﹣25 )﹣7;
(2) 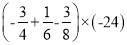 .
.
查看答案和解析>>
科目:初中数学 来源:贵州省遵义市桐梓县2016-2017学年七年级上学期期末考试数学试卷 题型:单选题
一个长方形的长为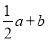 ,它的周长为3a+2b,则它的宽为( )
,它的周长为3a+2b,则它的宽为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:贵州省遵义市桐梓县2016-2017学年七年级上学期期末考试数学试卷 题型:单选题
国庆节长假期间,桐梓“黔北花海”——娄山关镇杉坪村以全域景观化的美景吸引了来自全国各地的大批游客,引爆了全县乡村旅游。据县旅游局统计,在国庆节长假期间全县共接待游客13.2万人次, “黔北花海”仅花海门票收入就达550余万元,全县旅游综合收入达3940万余元,创下历史新高.请将39 400 000用科学记数法表示为 ( )
A.  B.
B.  C.
C. 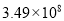 D.
D. 
查看答案和解析>>
科目:初中数学 来源:云南省双柏县2017-2018学年上学期七年级期末数学试卷 题型:单选题
计算:-5 -3×4的结果是( )
A. -17 B. -7 C. -8 D. -32
A 【解析】【解析】 -5 -3×4=-5-12=-17. 故选A.查看答案和解析>>
科目:初中数学 来源:江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型:解答题
如图,已知AD•AC=AB•AE.求证:△ADE∽△ABC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com