练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．tan30°的值为（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{3}}{2}$C．$\sqrt{3}$D．$\frac{\sqrt{3}}{3}$

    分析 根据特殊角三角函数值，可得答案．

    解答 解：tan30°=$\frac{\sqrt{3}}{3}$，
    故选：D．

    点评 本题考查了特殊角三角函数值，熟记特殊角三角函数值是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    11．下列运算正确的是（　　）
    A．$\sqrt{16}$=±4B．3-2=-$\frac{1}{9}$C．（$\sqrt{3}-\sqrt{2}$）2=1D．（$\sqrt{2}$-1）0=1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

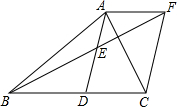    12．已知：在△ABC中，AD是BC边上的中线，点E是AD的中点；过点A作AF∥BC，交BE的延长线于F，连接CF．
    （1）求证：四边形ADCF是平行四边形；
    （2）填空：
    ①当AB=AC时，四边形ADCF是矩形；
    ②当∠BAC=90°时，四边形ADCF是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，一艘轮船从A港出发沿射线AB方形开往B港，在A港测得灯塔P在北偏东60°方向上，在B港测得灯塔P在北偏西25°方向上，已知AP=60海里，过P作PD⊥AB于点D．
    （1）求灯塔P到轮船航线的距离PD的长；
    （2）若轮船从A港到B港的航行时间为4小时，求轮船航行的平均速度（结果保留根号，参考数据：sin25°≈$\frac{21}{50}$，cos25°$≈\frac{9}{10}$，tan25°≈$\frac{7}{15}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．为了抓住2017年六一儿童节的商机，某商场决定购进甲、乙两种玩具进行销售，若购进甲种玩具1件，乙种玩具2件，需要160元，购进甲种玩具2件，乙种玩具3件，需要280元，购进甲、乙两种玩具每件各需要多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．若点A（-2，4），B（m，3）都在同一个正比例函数图象上，则m的值为-1.5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．在平面直角坐标系中，△A′B′C′是由△ABC平移后得到的，△ABC中任意一点P（x0，y0）经过平移后对应点为P′（x0+7，y0+2），若A′的坐标为（5，3），则它的对应的点A的坐标为（-2，1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，某飞机于空中探测某座山的高度，在点A处飞机的飞行高度是AF=3800米，从飞机上观测山顶目标C的俯角是45°，飞机继续以相同的高度飞行300米到B处，此时观测目标C的俯角是50°，求这座山的高度CD．
    （参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.20）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，一长度为10的线段AC的两个端点A、C分别在y轴和x轴的正半轴上滑动，以A为直角顶点，AC为直角边在第一象限内作等腰直角△ABC，连接BO．
    （1）求OB的最大值；
    （2）在AC滑动过程中，△OBC能否恰好为等腰三角形？若能，求出此时点A的坐标；若不能，请说明理由．

    查看答案和解析>>

    同步练习册答案