
【题目】(1)已知:如图,点E,A,C在同一条直线上,AB∥CD,AB=CE,AC=CD.求证:BC=ED.
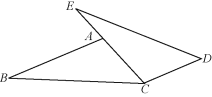
(2)如图,在⊙O中,过直径AB延长线上的点C做⊙O的一条切线,切点为D,若CD=4,CB=2.求:⊙O的半径.

【答案】(1)证明见解析;(2)3.
【解析】
试题分析:(1)利用“边边边”证明△ABC和△CED全等,根据全等三角形对应角相等可得∠CAB=∠DCE,再根据内错角相等,两直线平行证明即可;
(2)连接OD,根据切线的性质,∠ODC=90°,设OD=r,在RT△ODC中利用勾股定理即可解决.
试题解析:(1)在△ABC和△CED中,
∵AB=CE,AC=CD,BC=ED,∴△ABC≌△CED(SSS),
∴∠CAB=∠DCE,
∴AB∥CD.
(2)连接OD.
∵CD是⊙O切线,∴OD⊥CD,∴∠ODC=90°,
设半径为r,
在RT△ODC中,∵OD=r,OC=r+2,CD=4,
∴![]() ,
,
∴![]() ,
,
∴r=3,
∴⊙O的半径为3.



科目:初中数学 来源: 题型:
【题目】下列说法不能判断是正方形的是( )
A.对角线互相垂直且相等的平行四边形B.对角线互相垂直的矩形
C.对角线相等的菱形D.对角线互相垂直平分的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】比例尺为1:1000的图纸上某区域面积400cm2,则实际面积为 ( )
A.4×105 m2 B.4×104 m2 C.1.6×105 m2 D.2×104m2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若P是线段AB的黄金分割点(PA>PB),设AB=1,则PA的长约为( )
A. 0.191 B. 0.382 C. 0.5 D. 0.618
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
课题 | 测量教学楼高度 | |
方案 | 一 | 二 |
图示 |
|
|
测得数据 |
|
|
参考数据 | sin22°≈0.37,cos22°≈0.93, tan22°≈0.40,sin13°≈0.22, cos13°≈0.97,tan13°≈0.23 | sin32°≈0.53,cos32°≈0.85, tan32°≈0.62,sin43°≈0.68, cos43°≈0.73,tan43°≈0.93 |
请你选择其中的一种方案,求教学楼的高度(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径.半径OD垂直弦AC于点E.F是BA延长线上一点,![]() .
.
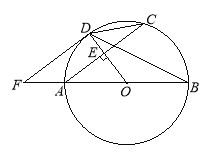
(1)判断DF与⊙O的位置关系,并证明;
(2)若AB=10,AC=8,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com