
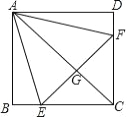
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有( )个
A. 4 B. 3 C. 2 D. 1
【答案】C
【解析】解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°.
∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,
![]() ,
,
Rt△ABE≌Rt△ADF(HL),
∴BE=DF(故①正确).
∠BAE=∠DAF,
∴∠DAF+∠DAF=30°,
即∠DAF=15°(故②正确),
∵BC=CD,
∴BC﹣BE=CD﹣DF,即CE=CF,
∵AE=AF,
∴AC垂直平分EF.(故③正确).
设EC=x,由勾股定理,得
EF=x,CG=![]() x,
x,
AG=AEsin60°=EFsin60°=2×CGsin60°=![]() x,
x,
∴AC=![]() ,
,
∴AB=![]() ,
,
∴BE=![]() ﹣x=
﹣x=![]() ,
,
∴BE+DF=x﹣x≠x,(故④错误),
∵S△CEF=![]() ,
,
S△ABE=![]() =
=![]() ,
,
∴2S△ABE=![]() =S△CEF,(故⑤正确).
=S△CEF,(故⑤正确).
综上所述,正确的有4个,
故选:A.
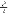


科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位,得到长方形A1B1C1D1,第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位,得到长方形A2B2C2D2…,第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向向右平移5个单位,得到长方形AnBnCnDn(n>2),若ABn的长度为2016,则n的值为( )
A. 400 B. 401 C. 402 D. 403
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )

A.AQ= PQ B.AQ=3PQ C.AQ=![]() PQ D.AQ=4PQ
PQ D.AQ=4PQ
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务. 已知每台GH型产品由4个G型装置和3个H型装置配套组成. 工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G 型装置的加工,且每人每天只能加工4个G型装置. 请问至少需要补充多少名新工人?
查看答案和解析>>
科目:初中数学 来源: 题型:
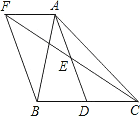
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
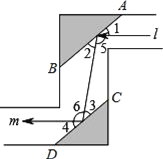
【题目】如图是潜望镜工作原理示意图,阴影部分是平行放置在潜望镜里的两面镜子.已知光线经过镜子反射时,有∠1=∠2,∠3=∠4,请解释进入潜望镜的光线l为什么和离开潜望镜的光线m是平行的?
请把下列解题过程补充完整.
理由:
∵AB∥CD(已知)
∴ (两直线平行,内错角相等)
∵∠1=∠2,∠3=∠4
∴∠1=∠2=∠3=∠4
∴180°﹣∠1﹣∠2=180°﹣∠3﹣∠4(平角定义)
即: (等量代换)
∴ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com