
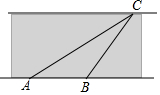
 在一次数学活动课上,老师带领学生去测一条东西流向的河宽(如图所示),小明同学在河南岸点A处观测到河对岸边有一点C,测得C在点A东偏北30°方向上,沿河岸向正东前行30米到达B处,测得C在点B东偏45°的方向上,请你根据以上数据,帮助小明同学计算出这条河的宽度.
在一次数学活动课上,老师带领学生去测一条东西流向的河宽(如图所示),小明同学在河南岸点A处观测到河对岸边有一点C,测得C在点A东偏北30°方向上,沿河岸向正东前行30米到达B处,测得C在点B东偏45°的方向上,请你根据以上数据,帮助小明同学计算出这条河的宽度. 分析 经过点C作CD⊥AB,则CD的长就是这条河的宽度.在构建两个直角三角形后,用已知角的正切值与AD、BD的长,然后根据二者之间的关系列方程,解答即可.
解答 解:如图,过点C作CD⊥AB于D点,设CD=x米,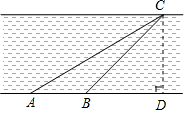
根据题意,知∠CAD=30°,∠CBD=45°,
∴BD=CD=x,
∵tan∠CAD=$\frac{CD}{AD}$,AB=30米,
∴$\frac{\sqrt{3}}{3}$=$\frac{x}{x+30}$,
解得:x=15$\sqrt{3}$+15,
答:这条河的宽度为(15+15$\sqrt{3}$)米.
点评 本题主要考查解直角三角形的应用,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案科目:初中数学 来源: 题型:解答题
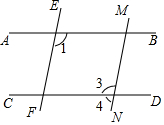 如图,直线AB,CD被直线EF,MN所截.
如图,直线AB,CD被直线EF,MN所截.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com