
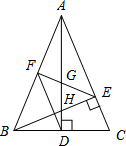
 如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确的有( )
如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确的有( )| A. | 1个 | B. | 2 个 | C. | 3 个 | D. | 4个 |
分析 由直角三角形斜边上的中线性质得出FD=$\frac{1}{2}$AB,证明△ABE是等腰直角三角形,得出AE=BE,证出FE=$\frac{1}{2}$AB,延长FD=FE,①正确;
证出∠ABC=∠C,得出AB=AC,由等腰三角形的性质得出BC=2CD,∠BAD=∠CAD=∠CBE,由ASA证明△AEH≌△BEC,得出AH=BC=2CD,②正确;
证明△ABD~△BCE,得出$\frac{BC}{AB}$=$\frac{BE}{AD}$,即BC•AD=AB•BE,再由等腰直角三角形的性质和三角形的面积得出BC•AD=$\sqrt{2}$AE2;③正确;
由F是AB的中点,BD=CD,得出S△ABC=2S△ABD=4S△ADF.④正确;即可得出结论.
解答 解:∵在△ABC中,AD和BE是高,
∴∠ADB=∠AEB=∠CEB=90°,
∵点F是AB的中点,
∴FD=$\frac{1}{2}$AB,
∵∠ABE=45°,
∴△ABE是等腰直角三角形,
∴AE=BE,
∵点F是AB的中点,
∴FE=$\frac{1}{2}$AB,
∴FD=FE,①正确;
∵∠CBE=∠BAD,∠CBE+∠C=90°,∠BAD+∠ABC=90°,
∴∠ABC=∠C,
∴AB=AC,
∵AD⊥BC,
∴BC=2CD,∠BAD=∠CAD=∠CBE,
在△AEH和△BEC中,$\left\{\begin{array}{l}{∠AEH=∠CEB}&{\;}\\{AE=BE}&{\;}\\{∠EAH=∠CBE}&{\;}\end{array}\right.$,
∴△AEH≌△BEC(ASA),
∴AH=BC=2CD,②正确;
∵∠BAD=∠CBE,∠ADB=∠CEB,
∴△ABD~△BCE,
∴$\frac{BC}{AB}$=$\frac{BE}{AD}$,即BC•AD=AB•BE,
∵$\sqrt{2}$AE2=AB•AE=AB•BE,BC•AD=AC•BE=AB•BE,
∴BC•AD=$\sqrt{2}$AE2;③正确;
∵F是AB的中点,BD=CD,∴
S△ABC=2S△ABD=4S△ADF.④正确;
故选:D.
点评 本题考查了相似三角形的判定与性质、全等三角形的判定与性质、直角三角形斜边上的中线性质、等腰三角形的判定与性质;本题综合性强,有一定难度,证明三角形相似和三角形全等是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
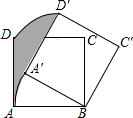 如图,正方形ABCD边长为3,将正方形ABCD绕点B顺时针旋转30°,得到正方形A′BC′D′,则图中阴影部分的面积是 $\frac{3}{4}π$.
如图,正方形ABCD边长为3,将正方形ABCD绕点B顺时针旋转30°,得到正方形A′BC′D′,则图中阴影部分的面积是 $\frac{3}{4}π$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2015年12月19日郑州机场T2航站楼正式启用,为了宣传T2航站楼,机场反面要印刷一批宣传材料,经招标,某印务公司中标,该印务公司提出3种方案:
2015年12月19日郑州机场T2航站楼正式启用,为了宣传T2航站楼,机场反面要印刷一批宣传材料,经招标,某印务公司中标,该印务公司提出3种方案:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
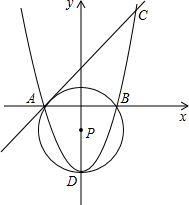 在平面直角坐标系中,已知点A(-2,0),B(2,0),C(3,5).
在平面直角坐标系中,已知点A(-2,0),B(2,0),C(3,5).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
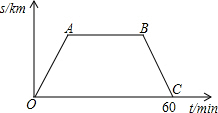 星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回家,图中的折线段OA-AB-BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )
星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回家,图中的折线段OA-AB-BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )| A. | 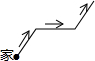 | B. | 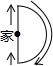 | C. | 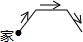 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com