
| 9 | a | b | c | -5 | 1 | … |
分析 (1)根据其中任意三个相邻格子中所填整数之和都相等,得出每三个数字一个循环,依次读下去,得c=9,a=-5,b=1,2015÷3=671余2,故2015个数为-5.
(2)通过分类讨论求出所有a、b的可能情况,求出结果即可,当取前19个格子中数字,这三个数,9出现了7次,-6和2各出现了6次,通过分类讨论求出所有s、t的可能情况,求出结果即可;
(3)计算三个格子和为5,而2015能被5整除,因此,n个格子中所填整数之和可以为2015.
解答 解:(1)∵任意三个相邻格子中所填整数之和都相等,
∴9+a+b=a+b+c,
解得c=9,
则a=-5,b=1,
所以,数据从左到右依次为9、-5、1、9、-5、1、…,
∵2015÷3=671…2,
∴第2015个格子中的整数与第2个格子中的数相同,为-5.
(2)|9-a|+|a-9|+|9-b|+|b-9|+|a-b|+|b-a|
=14+14+8+8+6+6
=56;
(3)能为2015.
理由:∵9-5+1=5,
2015÷5=403,
∴m=403×3=1209.
故答案为:9,-5.
点评 题目考查了数字的变化规律,通过表格中数字的变化,体会数字变化为学生们带来的快乐.题目整体较难,特别是(3)中的总结性求和,更能体现学生的解决问题能力.


科目:初中数学 来源: 题型:解答题
 为了美化环境,学校准备在如图所示的矩形ABCD空地上迸行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ.已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.
为了美化环境,学校准备在如图所示的矩形ABCD空地上迸行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ.已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
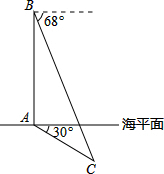 俄罗斯和中国2015年将在地中海海域和太平洋地区举行联合演习,我军自主演习时军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
俄罗斯和中国2015年将在地中海海域和太平洋地区举行联合演习,我军自主演习时军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
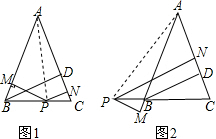 如图1,在△ABC中,AB=AC,BD是△ABC的高,P是BC边上一点,PN分别与直线AB,AC垂直,垂足分别为点M,N,求证:BD=PM+PN.
如图1,在△ABC中,AB=AC,BD是△ABC的高,P是BC边上一点,PN分别与直线AB,AC垂直,垂足分别为点M,N,求证:BD=PM+PN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com