
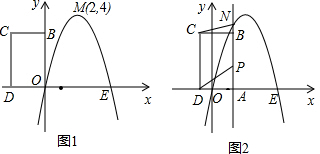
分析 (1)设抛物线解析式为y=a(x-2)2+4,将(0,0)代入求出a即可解决问题;
(2)①根据题意得出P点坐标,进而表示出N点坐标,分两种情形讨论当PN=0,即t=0或t=3时,P、N、C、D所构成的多边形为三角形,求出面积即可,当PN≠0时,P、N、C、D四点所构成的多边形是四边形,求出面积即可,即可得出最值;
②分两种情形分别以Q,M为直角顶点去分析求解即可求得答案.
解答 解:(1)设抛物线解析式为y=a(x-2)2+4,
把(0,0)代入解析式得a(0-2)2+4=0,
解得,a=-1,
∴函数解析式为y=-(x-2)2+4,即y=-x2+4x.
(2)存在.
①∵将矩形ABCD以每秒1个单位长度的速度从左图所示位置沿x轴的正方向匀速平行移动;
同时AB上一动点P也以相同的速度从点A出发向B匀速运动,设它们的运动时间为t秒,则点P的坐标为:(t,t),点N的坐标为:(t,-t2+4t),
∴PN=-t2+3t,
当PN=0,即t=0或t=3时,分别如图1,2,P、N、C、D所构成的多边形为三角形,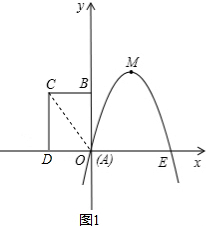
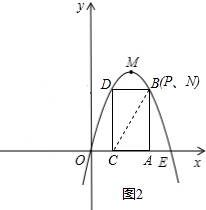
此时S=$\frac{1}{2}$DC•AD=$\frac{1}{2}$×3×2=3,
当PN≠0时,如图3,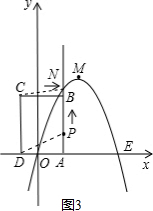
P、N、C、D四点所构成的多边形是四边形,
∵PN∥CD,AD⊥DC,
∴S=$\frac{1}{2}$(CD+PN)•AD,
=$\frac{1}{2}$[3+(-t2+3t)]×2,
=-t2+3t+3,
=-(t-$\frac{3}{2}$)2+$\frac{21}{4}$(0≤t≤3),
∴当t=$\frac{3}{2}$时,S最大=$\frac{21}{4}$>3,
综上可知P、N、C、D所构成的多边形的面积S有最大值,这个最大值为:$\frac{21}{4}$;
②如图4,作点M作MG⊥AB于点G,作MH⊥x轴于点H,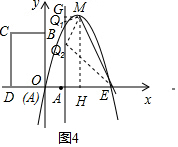
∵M(2,4),E(4,0),
则EH=2,MH=4,MG=2-1=1,
设点Q的坐标为(1,m),
若∠QME=90°,则△MGQ∽△MHE,
∴MG:GQ=MH:EH,
∴1:GQ=4:2,
解得:GQ=0.5,
∴m=4-0.5=3.5,
∴点Q的坐标为(1,3.5);
若∠MQE=90°,则△MGQ∽△QAE,
∴MG:GQ=AQ:AE,
∴1:(4-m)=m:3,
解得:m=1或m=3,
∴点Q的坐标为(1,1)或(1,3);
若∠QEM=90°,则点Q在BA的延长线上,不符合题意.
综上所述:点Q的坐标为:(1,3.5),(1,1),(1,3).
点评 此题属于二次函数的综合题、待定系数求函数解析式、平移变换、矩形的性质、相似三角形的判定与性质等知识,解题的关键是学会构建二次函数解决最值问题,学会用分类讨论的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
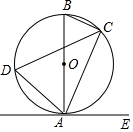 如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
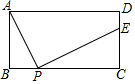 如图,矩形ABCD中,AB=4,BC=m(m>0).P为边BC上一动点(不与B、C重合),过P点作PE⊥AP交直线CD于E.
如图,矩形ABCD中,AB=4,BC=m(m>0).P为边BC上一动点(不与B、C重合),过P点作PE⊥AP交直线CD于E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,∠AOB=30°,点A的坐标为(2,0),过点A作AA1⊥OB,垂足为点A1,过A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2017的横坐标为( )
如图,在平面直角坐标系中,∠AOB=30°,点A的坐标为(2,0),过点A作AA1⊥OB,垂足为点A1,过A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2017的横坐标为( )| A. | $\frac{3}{2}$•($\frac{\sqrt{3}}{2}$)2015 | B. | $\frac{3}{2}$•($\frac{\sqrt{3}}{2}$)2016 | C. | $\frac{3}{2}$•($\frac{\sqrt{3}}{2}$)2017 | D. | $\frac{3}{2}$•($\frac{\sqrt{3}}{2}$)2018 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
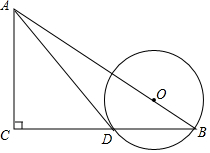 如图,在Rt△ABC中,∠ACB=Rt∠,点O在斜边AB上,以OB的长为半径的⊙O与BC交于点D,且AD与⊙O相切于点D.
如图,在Rt△ABC中,∠ACB=Rt∠,点O在斜边AB上,以OB的长为半径的⊙O与BC交于点D,且AD与⊙O相切于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com