由折叠的性质、矩形的性质与角平分线的性质,可证得CF=FM=DF;
易求得∠BFE=∠BFN,则可得BF⊥EN;易证得△BEN是等腰三角形,但无法判定是等边三角形;易求得BM=2EM=2DE,即可得EB=3EM,根据等高三角形的面积比等于对应底的比,即可求得答案.
解:∵四边形ABCD是矩形,
∴∠D=∠BCD=90°,
由折叠的性质可得:∠EMF=∠D=90°,DF=MF,
即FM⊥BE,CF⊥BC,
∵BF平分∠EBC,
∴CF=MF,
∴DF=CF;故①正确;
∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF,
∴∠BFM=∠BFC,
∵∠MFE=∠DFE=∠CFN,
∴∠BFE=∠BFN,
∵∠BFE+∠BFN=180°,
∴∠BFE=90°,
即BF⊥EN,故②正确;
∵在△DEF和△CNF中,
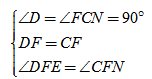
∴△DEF≌△CNF(ASA),
∴EF=FN,
∴BE=BN,
但无法求得△BEN各角的度数,
∴△BEN不一定是等边三角形;故③错误;
∵∠BFM=∠BFC,BM⊥FM,BC⊥CF,
∴BM=BC=AD=2DE=2EM,
∴BE=3EM,
∴S
△BEF=3S
△EMF=3S
△DEF;
故④正确.
故选B.



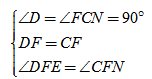


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案