
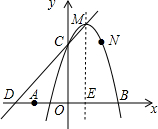
 ��ͼ����֪������y=-x2+2x+3�Ķ���ΪM���Ҿ�����N��2.3������x�ύ�����㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C��
��ͼ����֪������y=-x2+2x+3�Ķ���ΪM���Ҿ�����N��2.3������x�ύ�����㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C������ ��1�������䷽��������κ����������꣬�ٸ��������߽���ʽ���A��B��C�����ꣻ
��2������M��C����������ֱ��y=kx+t����ʽ���ó�D�����꣬���߶�AD����C��N���������֪CN��x�ᣬ����CN��֤��CN��ADƽ������ȣ��ж��ı���CDAN��ƽ���ı��Σ�
��3�����ڣ���ͼ��T��x1��y1����Q��x2��y2�����ֱ��T��Q��TF��y�ᣬQG��x�ᣬ����ֱ��TQ����ʽ�������߽���ʽ���ɵ�x1��y1��x2��y2֮��Ĺ�ϵ�������߶�TQΪֱ����Բǡ�ù�����ԭ��ʱ����TOQ=90�㣬���û����ϵ��֤��TOF�ס�QOG���������Ʊȵó��߶ι�ϵ�����x1��y1��x2��y2֮��Ĺ�ϵ��m��ֵ��
��� �⣺��1���������߽���ʽΪy=-1��x-1��2+4��
�ඥ��M�������ǣ���1��4����
y=-x2+2x+3��
��x=0����y=3����C��0��3����
��y=0����x=-1��3��
��A��-1��0����B��3��0����
�ʴ�Ϊ����-1��0������0��3������1��4����
��2���ı���CDAN��ƽ���ı��Σ�
���ɣ���C��0��3����M��1��4��������ֱ��y=kx+t�У���$\left\{\begin{array}{l}{t=3}\\{k+t=4}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=1}\\{t=3}\end{array}\right.$��
ֱ��CM����ʽΪ��y=x+3��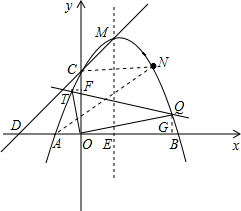
��D��-3��0����
��C��0��3����N��2��3����
��CN��x�ᣬ��CN=2-0=2��
�֡�A��-1��0����D��-3��0����
��AD=-1-��-3��=2��
���ı���CDAN��ƽ���ı��Σ�
��3�����ڣ�
��ͼ��T��x1��y1����Q��x2��y2�����ֱ��T��Q��TF��y�ᣬQG��x�ᣬ
����$\left\{\begin{array}{l}{y={-x}^{2}+2x+3}\\{y=mx+2}\end{array}\right.$��
��ã�x2+��m-2��x-1=0��
��x1+x2=2-m��x1x2=-1��
�����߶�TQΪֱ����Բǡ�ù�����ԭ��ʱ����TOQ=90�㣬
���TOF+��FOQ=��FOQ+��QOB=90�㣬
���TOF=��QOB������TFO=��QGO=90�㣬
���ԣ���TOF�ס�QOG��
��$\frac{TF}{QG}$=$\frac{OF}{OG}$��
��$\frac{-{x}_{1}}{{y}_{2}}$=$\frac{{y}_{1}}{{x}_{2}}$��
x1x2+y1y2=0��-1+��mx1+2����mx2+2��=0��
-1+m2x1x2+2m��x1+x2��+4=0��
-1-m2+2m��2-m��+4=0����������3m2-4m-3=0��
��ã�m=$\frac{2��\sqrt{13}}{3}$��
���� ���⿼���˶��κ������ۺ����ã��Լ����ý���ʽ����������������Ľ��㡢ƽ���ı��ε��ж����������������ε��ж������ʵ�֪ʶ����ȷ�ó���TOF�ס�QOG�ǽ���ؼ���


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪ƽ��ֱ������ϵ��A��2a-1��4����B��-3��3b+1����A��B���������y��Գ�
��ͼ����֪ƽ��ֱ������ϵ��A��2a-1��4����B��-3��3b+1����A��B���������y��Գ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 11 | B�� | 12 | C�� | 13 | D�� | ���϶��� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com