
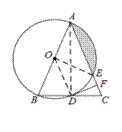
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

【答案】(1)证明见解析;(2)![]() -8.
-8.
【解析】试题分析:(1)连接AD、OD,如图,先利用圆周角定理得到∠ADB=90°,则根据等腰三角形的性质得BD=CD,于是可判断OD为△ABC的中位线,所以OD∥AC,则DF⊥OD,然后根据切线的判定定理可得DF是⊙O的切线;
(2)利用S阴影=S扇形AOE-S△AOE进而求出答案.
试题解析:(1)连接AD,OD.
∵AB是直径,
∴∠ADB=90°,∴AD⊥BC.
∵AB=AC ,
∴D是BC的中点.
∵O是AB的中点,
∴OD//AC.
∴∠ODF+∠DFA=180°
∵DF⊥AC,∴∠DFA=90°.
∴∠ODF=90°. ∴OD⊥DF
∴DF是⊙O的切线.
(2)连接OE
∵∠ADB=∠ADC=90°,∠DFC=∠DFA=90°,
∴∠DAC=∠CDF=22.5°
∵AB=AC,D是BC中点,
∴∠BAC=2∠DAC=2×22.5°=45°.
∵OA=OE,
∴∠OEA=∠BAC=45°.
∴∠AOE=90° .
∵AE=4![]() ,
,
∴OA=OE=4.
S阴影=S扇形AOE-S△AOE=4π-8.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=-x+b与反比例函数y=![]() (x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连接OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.
(x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连接OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.
(1)b=________(用含m的代数式表示);
(2)若S△OAF+S四边形EFBC=4,则m的值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.
(1)求sin∠EAC的值;
(2)求线段AH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计,2018年五·一期间,我市勺湖公园风景区接待中外游客的人数为86740人,将这个数字精确到百位可表示为 ( )
A. 8.6740×104 B. 0.8674×105 C. 8.67×104 D. 86.740×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某电视台的一档选秀节目中,有三位评委,每位评委在选手完成才艺表演后,出示“通过”(用√表示)或“淘汰”(用×表示)的评定结果,节目组规定:每位选手至少获得两位评委的“通过”才能晋级.
(1)请用树状图列举出选手A获得三位评委评定的各种可能的结果;
(2)求选手A晋级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com