
����Ŀ����ͼ�ף���ƽ��ֱ������ϵ�У�A��B������ֱ�Ϊ��4��0������0��3����������y= ![]() x2+bx+c������B���ҶԳ�����ֱ��x=��
x2+bx+c������B���ҶԳ�����ֱ��x=�� ![]() ��
��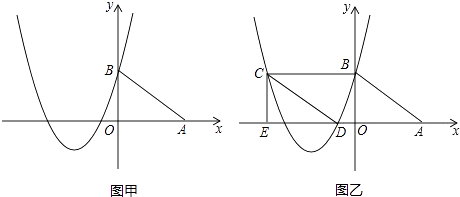
��1���������߶�Ӧ�ĺ�������ʽ��
��2����ͼ���С�ABO��x������ƽ�Ƶ���DCE����ͼ�ң������ı���ABCD������ʱ����˵����C�͵�D���ڸ��������ϣ�
��3���ڣ�2���У�����M���������ϵ�һ�����㣨��M�����C��D�غϣ���������M��MN��y�ύֱ��CD��N�����M�ĺ�����Ϊt��MN�ij���Ϊl����l��t֮��ĺ�������ʽ������tΪ��ֵʱ����M��N��C��EΪ������ı�����ƽ���ı��Σ����ο���ʽ��������y=ax2+bx+c��a��0���Ķ�������Ϊ���� ![]() ��
�� ![]() �����Գ�����ֱ��x=��
�����Գ�����ֱ��x=�� ![]() ����
����
���𰸡�
��1��
�⣺����������y= ![]() x2+bx+c��y�ύ�ڵ�B��0��3������ c=3��
x2+bx+c��y�ύ�ڵ�B��0��3������ c=3��
�������ߵĶԳ��� x=�� ![]() =��
=�� ![]() ��
��
��b=5a= ![]() ��
��
�������ߵĽ���ʽ��y= ![]() x2+
x2+ ![]() x+3��
x+3��
��2��
�⣺��A��4��0����B��0��3����
��OA=4��OB=3��AB= ![]() =5��
=5��
���ı���ABCD�����Σ���BC=AD=AB=5��
��C����5��3����D����1��0����
��C����5��3������y= ![]() x2+
x2+ ![]() x+3�У��ã�
x+3�У��ã� ![]() ������5��2+
������5��2+ ![]() ������5��+3=3�����Ե�C���������ϣ�
������5��+3=3�����Ե�C���������ϣ�
ͬ����֤����DҲ���������ϣ�
��3��
�⣺��ֱ��CD�Ľ���ʽΪ��y=kx+b�������⣬�У�
![]() �����
����� 
��ֱ��CD��y=�� ![]() x��
x�� ![]() ��
��
����MN��y�ᣬ�� M��t�� ![]() t2+
t2+ ![]() t+3������ N��t����
t+3������ N��t���� ![]() t��
t�� ![]() ����
����
�� t����5��t����1ʱ��l=MN=�� ![]() t2+
t2+ ![]() t+3��������
t+3�������� ![]() t��
t�� ![]() ��=
��= ![]() t2+
t2+ ![]() t+
t+ ![]() ��
��
�ک�5��t����1ʱ��l=MN=���� ![]() t��
t�� ![]() ������
������ ![]() t2+
t2+ ![]() t+3��=��
t+3��=�� ![]() t2��
t2�� ![]() t��
t�� ![]() ��
��
����M��N��C��EΪ������ı�����ƽ���ı��Σ�����MN��CE����MN=CE=3�����У�
![]() t2+
t2+ ![]() t+
t+ ![]() =3����ã�t1=��3+2
=3����ã�t1=��3+2 ![]() ��t2=��3��2
��t2=��3��2 ![]() ��
��
�� ![]() t2��
t2�� ![]() t��
t�� ![]() =3����ã�t=��3��
=3����ã�t=��3��
���ϣ�l= 
�ҵ�t=��3+2 ![]() ��t=��3��2
��t=��3��2 ![]() ��3ʱ����M��N��C��EΪ������ı�����ƽ���ı��Σ�
��3ʱ����M��N��C��EΪ������ı�����ƽ���ı��Σ�
����������1��������y=ax2+bx+c�У���0��c������������������y��Ľ��㣬x=�� ![]() �������ߵĶԳ��ᣬ�ݴ�ȷ������ϵ������2����֪A��B������꣬�ɹ��ɶ��������AB�ij������ı���ABCD�����Σ���ôAD=BC=AB���ɾݴ����C��D������꣬�ٴ��������ߵĽ���ʽ�н�����֤���ɣ���3������l��t֮��ĺ�������ʽʱ��Ҫ���������������������ֱ��CD�Ϸ�������������ֱ��CD�·����ȸ���ֱ��CD�������ߵĽ���ʽ����ʾ��M��N�����꣬����������IJΪl�ij�������M��N��C��EΪ������ı�����ƽ���ı���ʱ������CE��MN��y�ᣬ��ôCE����MN��ȣ���CE������l��t�ĺ�����ϵʽ�У������������������t��ֵ��
�������ߵĶԳ��ᣬ�ݴ�ȷ������ϵ������2����֪A��B������꣬�ɹ��ɶ��������AB�ij������ı���ABCD�����Σ���ôAD=BC=AB���ɾݴ����C��D������꣬�ٴ��������ߵĽ���ʽ�н�����֤���ɣ���3������l��t֮��ĺ�������ʽʱ��Ҫ���������������������ֱ��CD�Ϸ�������������ֱ��CD�·����ȸ���ֱ��CD�������ߵĽ���ʽ����ʾ��M��N�����꣬����������IJΪl�ij�������M��N��C��EΪ������ı�����ƽ���ı���ʱ������CE��MN��y�ᣬ��ôCE����MN��ȣ���CE������l��t�ĺ�����ϵʽ�У������������������t��ֵ��
�����㾫����������Ĺؼ������������ε����ʵ����֪ʶ���������ε������߶���ȣ����εĶԽ����ഹֱ������ÿһ���Խ���ƽ��һ��Խǣ����α������Խ��߷ֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ε�������������Խ��߳��Ļ���һ�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪��C���߶�AB�ϣ��߶�AC=10���ף�BC=6���ף���M��N�ֱ���AC��BC���е㣮
![]()
��1�����߶�MN�ij��ȣ�
��2�����ݵڣ�1����ļ�����̺ͽ������AC+BC=a�������������䣬��MN�ij��ȣ�
��3������P��Q�ֱ��A��Bͬʱ��������P��2cm/s���ٶ���AB�����˶����յ�ΪB����Q��1cm/s���ٶ���AB�����˶����յ�ΪA����һ���㵽���յ㣬��һ����Ҳ��ֹ֮ͣ�˶������˶�������ʱ��C��P��Q������һ��ǡ������������Ϊ�˵���߶ε��е㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��EFG�ա�NMH, ��F����M�Ƕ�Ӧ�ǣ�

��1��д����ȵ��߶�����ȵĽǣ�
��2����EF=2.1cm��FH=1.1cm��HM=3.3cm����MN��HG�ij���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A������Ϊ����2����1������B������Ϊ��0����2���������߶�ABƽ����A��B����λ�ã���A��������Ϊ��a��2������B��������Ϊ��1��b������a+b��ֵΪ��������
A. 0 B. 2 C. 4 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������y=3x��ͼ���뷴��������y= ![]() ��ͼ���ڵ�A��1��m���͵�B��
��ͼ���ڵ�A��1��m���͵�B�� 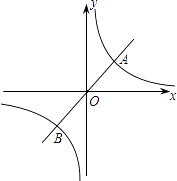
��1����m��ֵ�ͷ����������Ľ���ʽ��
��2���۲�ͼ��ֱ��д��ʹ������������ֵ���ڷ�����������ֵ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��AD=4��BC=12����E��BC���е㣮��P��Q�ֱ��DZ�AD��BC�ϵ����㣬���е�P��ÿ���1��λ���ȵ��ٶȴӵ�A�˶�����D���ٷ��ص�A��ͬʱ��Q��ÿ��2����λ���ȵ��ٶȴӵ�C�������B�˶���������һ�㵽���յ�ʱֹͣ�˶������˶�ʱ��tΪ_____��ʱ���Ե�A��P��Q��EΪ������ı�����ƽ���ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±���ӳ��x��y֮�����ij�ֺ�����ϵ���ָ����˼��ֿ��ܵĺ�����ϵʽ�� y=x+7��y=x��5��y=�� ![]() ��y=
��y= ![]() x��1
x��1
x | �� | ��6 | ��5 | 3 | 4 | �� |
y | �� | 1 | 1.2 | ��2 | ��1.5 | �� |
��1�����������ļ���ʽ����ѡ��һ������Ϊ�����ϱ�Ҫ��ĺ�������ʽ����
��2����˵����ѡ�������������ʽ�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���֪��A=80�㣬��B=60�㣬DE��BC����ô��CED�Ĵ�С�ǣ������� 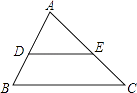
A.40��
B.60��
C.120��
D.140��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���̽��ɼס����������̶�����ɣ���֪���̶ӵ��������Ҫ60�죬�ҹ��̶ӵ��������Ҫ40��
��1�������̶�����30���ʣ�����ҹ��̶�����ɣ�����Ҫ��ʱ�� ����
��2�������̶�����20�죬�ҹ��̶��ٲμӣ��������̶�һ�������ʣ��Ĺ��̣������������ɸù�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com