
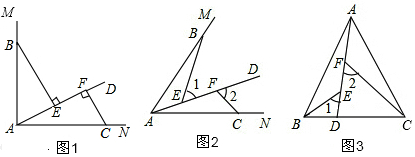
���� ��1����ͼ1������AAS֤����BAE�ա�ACF����BE=AF��
��2����ͼ2��������Ȼ�������ȸ�����֪�ǵĹ�ϵ�ã���ABE=��CAF����BAE=��ACF������ASA֤����BAE�ա�ACF����BE=AF��
��3����ͼ3����֤����BAE�ա�ACF����S��BAE=S��ACF����CD=2BD�ã�S��ABD=$\frac{1}{2}$S��ABC���Ӷ��ó����ۣ�
��� ֤������1����ͼ1���ߡ�MAN=90�㣬
���BAE+��CAF=90�㣬
��BE��AD��CF��AD��
���BEA=��AFC=90�㣬
���BAE+��EBA=90�㣬
���CAF=��EBA��
��AB=AC��
���BAE�ա�ACF��
��BE=AF��
��2����ͼ2����1���н�����Ȼ�����������ǣ�
�ߡ�1=��BAE+��ABE����1=��BAC��
���BAC=��BAE+��ABE��
�ߡ�BAC=��BAE+��CAF��
���ABE=��CAF��
�ߡ�1=��BAE+��ABE����2=��CAF+��ACF����1=��2��
���BAE=��ACF��
��AB=AC��
���BAE�ա�ACF��
��BE=AF��
��3����ͼ3���ߡ�2=��DAC+��ACF����2=��BAC��
���BAC=��DAC+��ACF��
�ߡ�BAC=��BAE+��DAC��
���BAE=��ACF��
�ߡ�1=��BAE+��ABE����2=��DAC+��ACF����1=��2��
���ABE=��DAC��
��AB=AC��
���BAE�ա�ACF��
��S��BAE=S��ACF��
��CD=2BD��S��ABC=15��
��S��ABD=$\frac{1}{3}$��15=5��
��S��ACF+S��BDE=S��BAE+S��BDE=S��ABD=5��
���ACF���BDE�����֮��Ϊ5��
���� �����������ε��ۺ��⣬�Ѷ����У�������������ȫ�ȵ��ж��������Լ������������������Ĺؼ��Ǹ��ݸ��Ե�����֤����BAE�ա�ACF��ͬʱ��ͬ���������У���ȷ�ױߵıȾ��Ƕ�Ӧ����ıȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
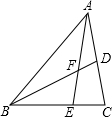 ��ͼ���ڡ�ABC�У�D��E�ֱ�ΪAC��BC����һ�㣬AE��BD���ڵ�F����֪AD=CD��BE=2CE���ҡ�ABC�����Ϊ60ƽ�����ף����ADF�����Ϊ6ƽ�����ף�����ѡ�BE=2CE����Ϊ��BE=nCE�������������䣬���ADF�����Ϊ$\frac{30}{2n+1}$ƽ�����ף��ú�n�Ĵ���ʽ��ʾ����
��ͼ���ڡ�ABC�У�D��E�ֱ�ΪAC��BC����һ�㣬AE��BD���ڵ�F����֪AD=CD��BE=2CE���ҡ�ABC�����Ϊ60ƽ�����ף����ADF�����Ϊ6ƽ�����ף�����ѡ�BE=2CE����Ϊ��BE=nCE�������������䣬���ADF�����Ϊ$\frac{30}{2n+1}$ƽ�����ף��ú�n�Ĵ���ʽ��ʾ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
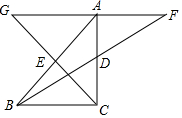 BD��CE�ǡ�ABC�����ߣ��ֱ���BD��CE���ӳ����Ͻ�ȡDF=DB��EG=EC������AF��AG����֤��AF=AG��
BD��CE�ǡ�ABC�����ߣ��ֱ���BD��CE���ӳ����Ͻ�ȡDF=DB��EG=EC������AF��AG����֤��AF=AG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | $\frac{1}{3}y$ | D�� | $-\frac{1}{3}y$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com