
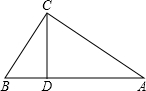
 已知,如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,CD⊥AB于D.
已知,如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,CD⊥AB于D.分析 (1)首先根据勾股定理求得直角三角形的第三边,进而得出其面积;
(2)根据直角三角形斜边上的高等于两条直角边的乘积除以斜边即可.
解答 解:(1)∵△ABC是直角三角形,AB=5cm,BC=3cm,
由勾股定理有:AC2=AB2-BC2.
∴AC=$\sqrt{{5}^{2}-{3}^{2}}$=4(cm),
∴S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$BC•AC=6(cm2);
(2)∵CD=$\frac{AC•BC}{AB}$=$\frac{12}{5}$(cm),
∴CD的长是$\frac{12}{5}$cm.
点评 此题主要考查了勾股定理,特别注意:直角三角形斜边上的高等于两条直角边的乘积除以斜边.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
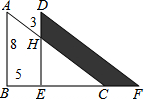 如图,原来是重叠的两个直角三角形,将其中一个三角形沿着BC方向平移线段BE的距离,就得到此图形,下列结论正确的有( )
如图,原来是重叠的两个直角三角形,将其中一个三角形沿着BC方向平移线段BE的距离,就得到此图形,下列结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7,24,25 | B. | 1.5,2,2.5 | C. | $\frac{5}{4}$,1,$\frac{3}{4}$ | D. | 40,50,60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com