
 如图,菱形ABCD和菱形BEFG的边长分别为3和2,∠A=60°,则图中阴影部分的面积是$\sqrt{3}$.
如图,菱形ABCD和菱形BEFG的边长分别为3和2,∠A=60°,则图中阴影部分的面积是$\sqrt{3}$. 分析 方法一:过点E作EQ⊥AD于点Q,记BC与DE交点为P,先证△BPE∽△ADE,从而得BP=$\frac{6}{5}$,继而知PG的长,在Rt△AQE中根据QE=AEsinA求得QE的长,最后由阴影部分的面积=$\frac{1}{2}$×PG×EQ可得答案;
方法二:连接BD,过点D作DQ⊥EG,交EG延长线于点Q,作BP⊥GE,利用菱形的性质证BD∥GE得DQ=BP,从而由S阴影=$\frac{1}{2}$GE•DQ=$\frac{1}{2}$GE•BP=S△BGE可得答案.
解答 解:方法一:过点E作EQ⊥AD于点Q,记BC与DE交点为P,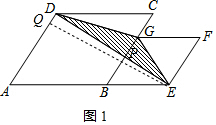
∵四边形ABCD是菱形,
∴BC∥AD,
∴△BPE∽△ADE,
∴$\frac{BP}{AD}$=$\frac{EB}{EA}$,即$\frac{BP}{3}$=$\frac{2}{5}$,
解得:BP=$\frac{6}{5}$,
∴PG=BG-BP=2-$\frac{6}{5}$=$\frac{4}{5}$,
在Rt△AQE中,∵∠A=60°,
∴QE=AEsinA=$\frac{5\sqrt{3}}{2}$,
∴阴影部分的面积=$\frac{1}{2}$×PG×EQ=$\sqrt{3}$,
方法二:如图2,连接BD,过点D作DQ⊥EG,交EG延长线于点Q,作BP⊥GE,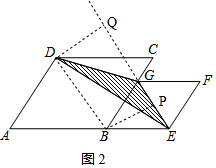
∵∠A=60°,且四边形ABCD和四边形BEFG均为菱形,
∴∠DBA=∠GEB=60°,
∴BD∥GE,
∴DQ=BP,
∵BE=BG=2、∠GBE=∠A=60°,
∴△BGE为等边三角形,
则S阴影=$\frac{1}{2}$GE•DQ=$\frac{1}{2}$GE•BP=S△BGE=$\frac{\sqrt{3}}{4}$×22=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题主要考查的是相似三角形的性质和判定,求得DN和BH的长是解题的关键.


科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,∠BCA=90°,∠A=30°.
已知:如图,在△ABC中,∠BCA=90°,∠A=30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | sin 45°+cos45°=1 | B. | 2tan30°=tan60° | ||
| C. | 2sin60°=tan45° | D. | sin230°=$\frac{1}{2}$cos60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2289×103 | B. | 2.289×103 | C. | 2.289×106 | D. | 2.289×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$ | B. | $\sqrt{3-π}$ | C. | $\sqrt{{a^2}+1}$ | D. | $\sqrt{\frac{1}{3}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{5}{4}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com