
【题目】如图,在四边形ABCD中,∠B=∠D=90°,AE,CF分别平分∠BAD及∠DCB,则AE∥FC吗?为什么?

科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F.
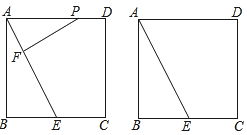
(1)求证:△PFA∽△ABE;
(2)当点P在射线AD上运动时,设PA=x,是否存在实数x,使以P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里共有2个黄球和3个白球,每个球除颜色外都相同,小亮从袋子中任意摸出一个球,结果是白球,则下面关于小亮从袋中摸出白球的概率和频率的说明正确的是( )
A. 小亮从袋中任意摸出一个球,摸出白球的概率是1
B. 小亮从袋中任意摸出一个球,摸出白球的概率是0
C. 在这次实验中,小亮摸出白球的频率是1
D. 由这次实验的频率去估计小亮从袋中任意摸出一个球,摸出白球的概率是1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )

A.9![]() B.12C.8D.8
B.12C.8D.8![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的方程x2-ax+a2-3=0至少有一个正根,则实数a的取值范围是( )
A. -2<a<2 B. ![]() <a≤2 C.
<a≤2 C. ![]() <a≤2 D.
<a≤2 D. ![]() ≤a≤2
≤a≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
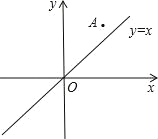
【题目】如图,已知点A(2,3)和直线y=x,
(1)点A关于直线y=x的对称点为点B,点A关于原点(0,0)的对称点为点C;写出点B、C的坐标;
(2)若点D是点B关于原点(0,0)的对称点,判断四形ABCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班总数相等.此时有学生建议,可以通过考察数据中的其他信息作为参考.
请你回答下列问题:
(1)填空:甲班的优秀率为 ,乙班的优秀率为 ;
(2)填空:甲班比赛数据的中位数为 ,乙班比赛数据的中位数为 ;
(3)填空:估计两班比赛数据的方差较小的是 班(填甲或乙)
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com