

 ĆėŹ±£¬S×ī“óÖµĪŖ
ĆėŹ±£¬S×ī“óÖµĪŖ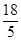 cm2;
cm2;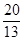
 s»ņ
s»ņ s»ņ
s»ņ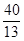 sŹ±£¬”÷APQŹĒµČŃüČż½ĒŠĪ£®
sŹ±£¬”÷APQŹĒµČŃüČż½ĒŠĪ£®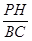 =
=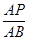 £¬“Ó¶ųĒó³öAB£¬ŌŁøł¾Ż
£¬“Ó¶ųĒó³öAB£¬ŌŁøł¾Ż =
=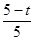 £¬µĆ³öPH=3©
£¬µĆ³öPH=3©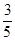 t£¬Ōņ”÷AQPµÄĆ껿ĪŖ£ŗ
t£¬Ōņ”÷AQPµÄĆ껿ĪŖ£ŗ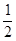 AQ•PH=
AQ•PH=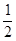 t£Ø3©
t£Ø3©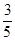 t£©£¬×īŗó½ųŠŠÕūĄķ¼“æÉµĆ³ö“š°ø£»
t£©£¬×īŗó½ųŠŠÕūĄķ¼“æÉµĆ³ö“š°ø£»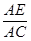 =
=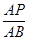 £¬Ēó³öAE=©
£¬Ēó³öAE=©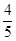 t+4£¬ŌŁøł¾ŻQE=AE©AQ£¬QE=
t+4£¬ŌŁøł¾ŻQE=AE©AQ£¬QE=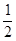 QCµĆ³ö©
QCµĆ³ö©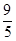 t+4=©
t+4=©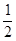 t+2£¬ŌŁĒót¼“æÉ£»
t+2£¬ŌŁĒót¼“æÉ£»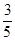 t+3£¬Óė£Ø2£©Ķ¬ĄķµĆ£ŗQD=©
t+3£¬Óė£Ø2£©Ķ¬ĄķµĆ£ŗQD=©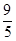 t+4£¬“Ó¶ųĒó³öPQ=
t+4£¬“Ó¶ųĒó³öPQ=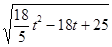 £¬
£¬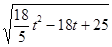 =t£¬¢Ūµ±PQ=AP£¬¼“
=t£¬¢Ūµ±PQ=AP£¬¼“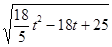 =5©t£¬ŌŁ·Ö±š¼ĘĖć¼“æÉ
=5©t£¬ŌŁ·Ö±š¼ĘĖć¼“æÉ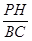 =
=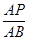 £¬
£¬ =
=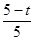 £¬
£¬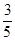 t£¬
t£¬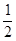 ”ĮAQ”ĮPH=
”ĮAQ”ĮPH=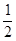 ”Įt”Į£Ø3©
”Įt”Į£Ø3©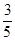 t£©=©
t£©=©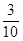 £Øt©
£Øt© £©2+
£©2+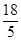 £¬
£¬ ĆėŹ±£¬S×ī“óÖµĪŖ
ĆėŹ±£¬S×ī“óÖµĪŖ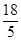 cm2£®
cm2£®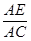 =
=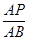 £¬
£¬ =
=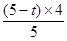 =©
=©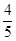 t+4
t+4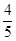 t+4©t=©
t+4©t=©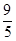 t+4£¬
t+4£¬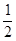 QC=
QC=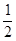 £Ø4©t£©=©
£Ø4©t£©=©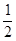 t+2£¬
t+2£¬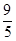 t+4=©
t+4=©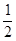 t+2£¬
t+2£¬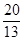 £¬
£¬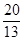 £¼4£¬
£¼4£¬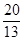 s£»
s£»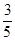 t+3£¬Óė£Ø2£©Ķ¬ĄķµĆ£ŗQD=AD©AQ=©
t+3£¬Óė£Ø2£©Ķ¬ĄķµĆ£ŗQD=AD©AQ=©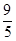 t+4
t+4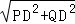 =
=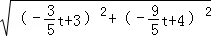 =
=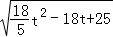 £¬
£¬ £»
£»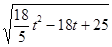 =tŹ±£¬½āµĆ£ŗt2=
=tŹ±£¬½āµĆ£ŗt2= £¬t3=5£»
£¬t3=5£»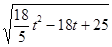 =5©tŹ±£¬½āµĆ£ŗt4=0£¬t5=
=5©tŹ±£¬½āµĆ£ŗt4=0£¬t5=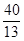 £»
£» s»ņ
s»ņ s»ņ
s»ņ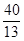 sŹ±£¬”÷APQŹĒµČŃüČż½ĒŠĪ£®
sŹ±£¬”÷APQŹĒµČŃüČż½ĒŠĪ£®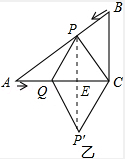
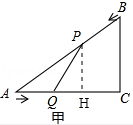



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗµ„Ń”Ģā
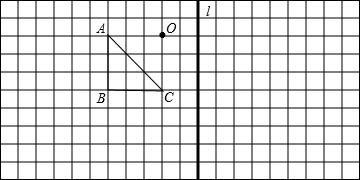
ČēĶ¼£¬ĻĀĮŠŠĪדµÄ±ßæņ£¬²»ĻąĖʵďĒ£Ø””””£©
|
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗµ„Ń”Ģā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗĢīæÕĢā

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com