
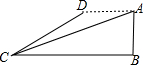
 如图,飞机的高度AB=1000千米,从飞机上测得地面着陆点C的俯角为18°,飞机水平飞行一段距离后,到达D点,此时测得地面着陆点C的俯角为30°,求飞机飞行的距离AD的长(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,tan18°≈0.32)
如图,飞机的高度AB=1000千米,从飞机上测得地面着陆点C的俯角为18°,飞机水平飞行一段距离后,到达D点,此时测得地面着陆点C的俯角为30°,求飞机飞行的距离AD的长(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,tan18°≈0.32) 分析 过点D作DE⊥BC于点E,先由锐角三角函数的定义得出BC的长,再求出CE的长,根据AD=BE=BC-CE即可得出结论.
解答 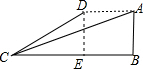 解:过点D作DE⊥BC于点E,
解:过点D作DE⊥BC于点E,
∵AB⊥BC,AD∥BC,
∴四边形ABED是矩形.
∵∠ACB=18°,AB=1000千米,
∴BC=$\frac{AB}{tan18°}$=$\frac{1000}{tan18°}$.
∵∠BCD=30°,
∴CE=$\frac{DE}{tan30°}$=$\frac{1000}{\frac{\sqrt{3}}{3}}$=1000$\sqrt{3}$,
∴AD=BE=BC-CE=$\frac{1000}{tan18°}$-1000$\sqrt{3}$≈$\frac{1000}{0.32}$-1730=3125-1730=1395(千米).
答:飞机飞行的距离AD的长为1395千米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是3$\sqrt{2}$cm.
如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是3$\sqrt{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
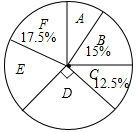 某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)| 选修课 | A | B | C | D | E | F |
| 人数 | 20 | 30 |
| A. | 这次被调查的学生人数为200人 | |
| B. | 扇形统计图中E部分扇形的圆心角为72° | |
| C. | 被调查的学生中最想选F的人数为35人 | |
| D. | 被调查的学生中最想选D的有55人 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠C=90°,CA=CB=4,将△ABC翻折,使得点B与边AC的中点M重合,如果折痕与边AB的交点为E,那么BE的长为$\frac{5\sqrt{2}}{3}$.
如图,在Rt△ABC中,∠C=90°,CA=CB=4,将△ABC翻折,使得点B与边AC的中点M重合,如果折痕与边AB的交点为E,那么BE的长为$\frac{5\sqrt{2}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>-7 | B. | k≥-7 | C. | k≥0 | D. | k≥1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com