
【题目】已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连结AE交射线DC于点F,将△ABE沿直线AE翻折,点B落在点B1处.

(1)如图1,若点E在线段BC上,求CF的长;
(2)求sin∠DAB1的值.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() .
.
【解析】
试题分析:(1)利用平行线性质以及线段比求出CF的值;
(2)本题要分两种方法讨论:①若点E在线段BC上;②若点E在边BC的延长线上.需运用勾股定理求出与之相联的线段;
试题解析:(1)∵AB∥DF,
∴![]() ,
,
∵BE=2CE,AB=3,
∴![]() ,
,
∴CF=![]() ;
;
(2)①若点E在线段BC上,如图1,设直线AB1与DC相交于点M.
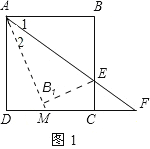
由题意翻折得:∠1=∠2.
∵AB∥DF,
∴∠1=∠F,
∴∠2=∠F,
∴AM=MF.
设DM=x,则CM=3-x.
又∵CF=1.5,
∴AM=MF=![]() -x,
-x,
在Rt△ADM中,AD2+DM2=AM2,
∴32+x2=(![]() -x)2,
-x)2,
∴x=![]()
∴DM=![]() ,AM=
,AM=![]() ,
,
∴sin∠DAB1=![]() ;
;
②若点E在边BC的延长线上,如图2,设直线AB1与CD延长线相交于点N.
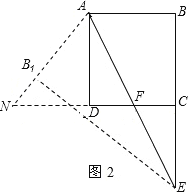
同理可得:AN=NF.
∵BE=2CE,
∴BC=CE=AD.
∵AD∥BE,
∴![]() ,
,
∴DF=FC=![]() ,
,
设DN=x,则AN=NF=x+![]() .
.
在Rt△ADN中,AD2+DN2=AN2,
∴32+x2=(x+![]() )2,
)2,
∴x=![]() .
.
∴DN=![]() ,AN=
,AN=![]()
sin∠DAB1=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC的平分线交CD于点E.
(1)若∠A=70°,求∠ABE的度数;
(2)若AB∥CD,且∠1=∠2,判断DF和BE是否平行,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图坐标系中,O(0,0) ,A(6,6![]() ),B(12,0).将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(12,0).将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=![]() ,则CE : DE的值是______.
,则CE : DE的值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=a(x-m)2+k与y2=a(x+m)2+k(m≠0)关于y轴对称,我们称y1与y2互为“和谐抛物线”.请写出抛物线y=-4x2+6x+7的“和谐抛物线” .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某件商品的成本价为a元,按成本价提高40%后标价,又以8折销售,则这件商品的售价为( )
A. 1.02a元 B. 1.12a元 C. 1.28a元 D. 0.72a元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图2菱形ABCD四个顶点都在坐标轴上,对角线AC、BD交于原点O,DF垂直AB交AC于点G,反比例函数![]() ,经过线段DC的中点E,若BD=4,则AG的长为( )
,经过线段DC的中点E,若BD=4,则AG的长为( )

A.![]() B.
B.![]() +2 C.2
+2 C.2![]() +1 D.
+1 D.![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】股市规定:股票每天的涨、跌幅均不超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停.若一支股票某天跌停,之后两天时间又涨回到原价,若这两天此股票股价的平均增长率为x,则x满足的方程是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com