练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，E，F分别是菱形ABCD的边AB，AD的中点，且AB＝5，AC＝6.

    （1）求对角线BD的长；

    （2）求证：四边形AEOF为菱形.

    【答案】（1）DB＝8；（2）见解析.

    【解析】（1）利用菱形的性质结合勾股定理得出OB的长即可得出DB的长；

    （2）利用三角形中位线定理进而得出四边形AEOF是平行四边形，再利用菱形的判定方法得出即可．

    （1）∵四边形ABCD是菱形，

    ∴AC⊥DB，AO＝AC，BO＝DB.

    ∵AC＝6，∴AO＝3.

    ∵AB＝5，

    ∴OB＝＝4，

    ∴DB＝8；

    （2）∵E，O分别是BA，BD的中点，

    ∴OE∥AD，OE＝AD，即OE∥AF，OE＝AF，

    ∴四边形AEOF是平行四边形.

    又∵AB＝AD，E，F分别是AB，AD的中点，

    ∴AE＝AF，

    ∴平行四边形AEOF是菱形.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】先化简,再求值: ，其中x的值从不等式组的整数解中选取.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，AB=AD=2，∠A=60°，BC=，CD=3．

    （1）求∠ADC的度数；

    （2）求四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在棋盘中建立如图的直角坐标系，三颗棋子A，O，B的位置如图，它们分别是（﹣1，1），（0，0）和（1，0）．
    （1）如图2，添加棋子C，使A，O，B，C四颗棋子成为一个轴对称图形，请在图中画出该图形的对称轴；
    （2）在其他格点位置添加一颗棋子P，使A，O，B，P四颗棋子成为一个轴对称图形，请直接写出棋子P的位置的坐标．（写出2个即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】等边三角形ABC的边长为6，在AC，BC边上各取一点E，F，连接AF，BE相交于点P．

    （1）若AE=CF；
    ①求证：AF=BE，并求∠APB的度数；
    ②若AE=2，试求APAF的值；
    （2）若AF=BE，当点E从点A运动到点C时，试求点P经过的路径长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】材料1：反射定律

    当入射光线AO照射到平面镜上时，将遵循平面镜反射定律，即反射角（∠BOM）的大小等于入射角（∠AOM）的大小，显然，这两个角的余角也相等，其中法线（OM）与平面镜垂直，并且满足入射光线、反射光线（OB）与法线在同一个平面．

    材料2：平行逃逸角

    对于某定角∠AOB=α（0°＜α＜90°），点P为边OB上一点，从点P发出一光线PQ（射线），其角度为∠BPQ=β（0°＜β＜90°），当光线PQ接触到边OA和OB时会遵循反射定律发生反射，当光线PQ经过n次反射后与边OA或OB平行时，称角为定角α的n阶平行逃逸角，特别地，当光线PQ直接与OA平行时，称角β为定角α的零阶平行逃逸角．

    （1）已知∠AOB=α=20°，

    ①如图1，若PQ∥OA，则∠BPQ=　 　°，即该角为α的零阶平行逃逸角；

    ②如图2，经过一次反射后的光线P1Q∥OB，此时的∠BPP1为α的平行逃逸角，求∠BPP1的大小；

    ③若经过两次反射后的光线与OA平行，请补全图形，并直接写出α的二阶平行逃逸角为　 　°；

    （2）根据（1）的结论，归纳猜想对于任意角α（0°＜α＜90°），其n（n为自然数）阶平行逃逸角β=　 　（用含n和a的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线y=3x﹣3分别交x轴、y轴于A、B两点，抛物线y=x2+bx+c经过A、B两点，点C是抛物线与x轴的另一个交点（与A点不重合）．

    （1）求抛物线的解析式：
    （2）求△ABC的面积；
    （3）在抛物线的对称轴上，是否存在点M，使△ABM周长最短？若不存在，请说明理由；若存在，求出点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某个体经营户销售同一型号的A、B两种品牌的服装，平均每月共销售60件，已知两种品牌的成本和利润如表所示，设平均每月的利润为y元，每月销售A品牌x件．
    （1）写出y关于x的函数关系式．
    （2）如果每月投入的成本不超过6500元，所获利润不少于2920元，不考虑其他因素，那么销售方案有哪几种？
    （3）在（2）的条件下要使平均每月利润率最大，请直接写出A、B两种品牌的服装各销售多少件？

    A

    B

    成本（元/件）

    120

    85

    利润（元/件）

    60

    30

    查看答案和解析>>

    科目：初中数学 来源： 题型：

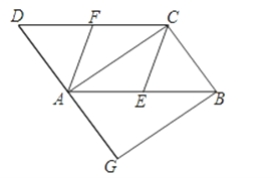
    【题目】如图，在ABCD中，E、F分别为边AB、CD的中点，AC是对角线，过点B作BG∥AC交DA的延长线于点G．

    （1）求证：CE∥AF；

    （2）若∠G=90°，求证：四边形CEAF是菱形．

    查看答案和解析>>

    同步练习册答案