练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．若点M（a-2，2a+3）是x轴上的点，求a的值．
    解：∵点M（a-2，2a+3）是x轴上的点，∴纵坐标2a+3是0，
    ∴2a+3=0，∴a=-$\frac{3}{2}$．

    分析 根据x轴上的点的纵坐标为0解答即可．

    解答 解：∵点M（a-2，2a+3）是x轴上的点，
    ∴纵坐标2a+3是0，
    ∴2a+3=0，
    ∴a=-$\frac{3}{2}$．
    故答案为：0；-$\frac{3}{2}$．

    点评 本题考查了点的坐标，熟记x轴上的点的纵坐标为0是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．化简：2$\sqrt{x}$-$\frac{\sqrt{x-2}}{x-2}$÷$\sqrt{\frac{x}{{x}^{3}-2{x}^{2}}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．下面用科学记数法表示的数，原来是什么数？地球上的海洋面积约为3.6×108平方千米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．把65°28′45″化成度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．化简：
    （1）（-ab+2）（5ab-3）-ab（1-ab）；
    （2）（-2x）•（x2-5x+6）-4x（2x2-3x+1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，在东西方向的海岸线一观测点A处，某时刻测得一艘匀速直线航行的渔船位于A的东偏北30°方向，且与点A相距20$\sqrt{3}$千米的B处，经过40分钟，该渔船在与A相距20千米的C处靠岸，求该渔船航行的速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．已知$\frac{1}{1×\sqrt{2}+2\sqrt{1}}$+$\frac{1}{2\sqrt{3}+3\sqrt{2}}$+…+$\frac{1}{n\sqrt{n+1}+（n+1）\sqrt{n}}$的值大于$\frac{19}{20}$，小于$\frac{20}{21}$，则正整数n的最大值与最小值的差等于134．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

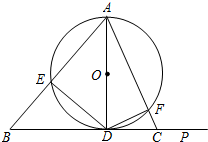    4．如图，在锐角△ABC中，AB＞AC，AD⊥BC于D，以AD为直径的⊙O分别交AB，AC于E，F，连结DE，DF．
    （1）求∠EDF的度数；
    （2）已知P是射线DC上一个动点，当点P运动到PD=BD时，连结AP，交⊙O于G，连结DG．若∠BAC=70°，∠APB=50°，⊙O 的半径长为1，
    ①求证：∠EDG+∠BAG=180°； 
    ②求劣弧DF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：
    （1）$（-\frac{6}{5}）-7-（-3.2）+（-1）$；
    （2）$（-\frac{6}{7}）-（-\frac{1}{5}）-（-\frac{1}{7}）+（-1\frac{1}{5}）$．

    查看答案和解析>>

    同步练习册答案