
【题目】已知:△ABC中,∠C=90°.
(1)a=6,b=2![]() ,求∠A,∠B,c;
,求∠A,∠B,c;
(2)a=24,c=24![]() ,求∠A,∠B,b.
,求∠A,∠B,b.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤2元的利润出售一种水果,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.2元,每天可多售出40斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是________斤(用含x的代数式表示);
(2)销售这种水果要想每天赢利300元,张阿姨需将这种水果每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
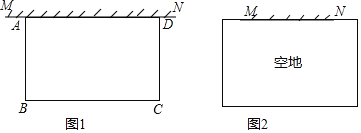
【题目】空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为100米.
(1)已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图1,求所利用旧墙AD的长;
(2)已知0<α<50,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
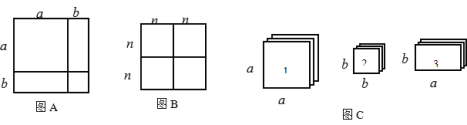
【题目】 我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:图A可以用来解释![]() ,实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解.
,实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解.
(1)图B可以解释的代数恒等式是 ;
(2)现有足够多的正方形和矩形卡片,如图C:
①若要拼出一个面积为(3a+b)(a+2b)的矩形,则需要1号卡片 张,2号卡片 张,3号卡片 张;
②试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形,使该矩形的面积为6a2+7ab+2b2,并利用你画的图形面积对6a2+7ab+2b2进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
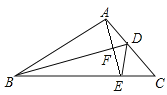
【题目】如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D,连接DE.
(1)若△ABC的周长为18,△DEC的周长为6,求AB的长;
(2)若![]() ,
,![]() ,求
,求![]() 度数.
度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克,以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(1)求第一次水果的进价是每千克多少元?
(2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.“寒假”期间,某校小记者随机调查了某地区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:

(1)求这次调查的家长人数,并补全图1;
(2)求图2中表示家长“赞成”的圆心角的度数;
(3)已知某地区共6500名家长,估计其中反对中学生带手机的大约有多少名家长?
查看答案和解析>>
科目:初中数学 来源: 题型:
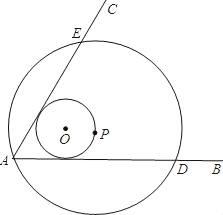
【题目】如图∠BAC=60°,半径长1的⊙O与∠BAC的两边相切,P为⊙O上一动点,以P为圆心,PA长为半径的⊙P交射线AB、AC于D、E两点,连接DE,则线段DE长度的最大值为( )
A. 3 B. 6 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
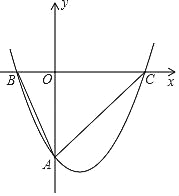
【题目】如图,经过点A(0,﹣4)的抛物线y=![]() x2+bx+c与x轴相交于点B(﹣2,0)和C,O为坐标原点.
x2+bx+c与x轴相交于点B(﹣2,0)和C,O为坐标原点.
(1)求抛物线解析式;
(2)将抛物线y=![]() x2+bx+c向上平移
x2+bx+c向上平移![]() 个单位长度,再向左平移m(m>0)个单位长度,得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围.
个单位长度,再向左平移m(m>0)个单位长度,得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com