
【题目】某商店决定购进A、B两种纪念品.若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑到市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B 种纪念品可获利润30元,在(2)的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
【答案】(1)购进一件A种纪念品需要50元,购进一件B种纪念品需要100元
(2)共有6种进货方案
(3)当购进A种纪念品160件,B种纪念品20件时,可获最大利润,最大利润是3800元
【解析】
(1)设我校购进一件A种纪念品需要a元,购进一件B种纪念品需要b元,根据条件建立二元一次方程组求出其解即可;
(2)设我校购进A种纪念品x个,购进B种纪念品y个,根据条件的数量关系建立不等式组求出其解即可;
(3)设总利润为W元,根据总利润=两种商品的利润之和建立解析式,由解析式的性质就可以求出结论.
(1)设我校购进一件A种纪念品需要a元,购进一件B种纪念品需要b元,由题意,得
![]() ,
,
∴解方程组得:
![]()
答:购进一件A种纪念品需要50元,购进一件B种纪念品需要100元.
(2)设我校购进A种纪念品x个,购进B种纪念品y个,由题意,得
则![]() ,
,
解得![]() ,
,
解得:20≤y≤25
∵y为正整数
∴y=20,21,22,23,24,25
答:共有6种进货方案;
(3)设总利润为W元,由题意,得
W=20x+30y=20(200-2 y)+30y,
=-10y+4000(20≤y≤25)
∵-10<0,
∴W随y的增大而减小,
∴当y=20时,W有最大值
W最大=-10×20+4000=3800(元)
答:当购进A种纪念品160件,B种纪念品20件时,可获最大利润,最大利润是3800元.


科目:初中数学 来源: 题型:
【题目】下列命题:①若![]() ,则
,则![]() ;②直角三角形的两个锐角互余:③如果
;②直角三角形的两个锐角互余:③如果![]() ,那么
,那么![]() ④
④![]() 个角都是直角的四边形是正方形.其中,原命题和逆命题均为真命题的有( )
个角都是直角的四边形是正方形.其中,原命题和逆命题均为真命题的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点P是(不与点A,B重合)为半圆上一点.将图形沿BP折叠,分别得到点A’,O’.设∠ABP=α.

(1)当α=10°时,∠ABA’= ____度;
(2)当点O’落在弧![]() 上时,求出α的度数.
上时,求出α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名采购员同去一家饲料公司购买两次饲料.两次饲料的价格分别为![]() 元/千克和
元/千克和![]() 元/千克(
元/千克(![]() 、
、![]() 都为正数,且
都为正数,且![]() ),两名采购员的购货方式不同,其中甲每次购买800千克;乙每次用去800元,而不管购买多少饲料.
),两名采购员的购货方式不同,其中甲每次购买800千克;乙每次用去800元,而不管购买多少饲料.
(1)用含![]() 、
、![]() 的代数式表示甲、乙两名采购员两次购买饲料的平均单价各是多少?
的代数式表示甲、乙两名采购员两次购买饲料的平均单价各是多少?
(2)若规定:谁两次购买饲料的平均单价低,谁的购货方式合算,请你判断甲、乙两名采购员购货方式哪个更合算?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的曲线是函数y=![]() (m为常数)图象的一支.
(m为常数)图象的一支.
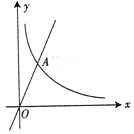
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例
函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
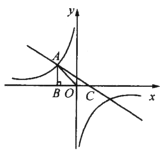
【题目】如图,已知反比例函数![]() (k<0)的图像经过点A(
(k<0)的图像经过点A(![]() ,m),过点A作AB⊥x轴于点,且△AOB的面积为
,m),过点A作AB⊥x轴于点,且△AOB的面积为![]() .
.
(1)求k和m的值;
(2)若一次函数y=ax+1的图像经过点A,并且与x轴相交于点C,求∠ACO的度数及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用相同的小正方形按照某种规律进行摆放.根据图中小正方形的排列规律,猜想第![]() 个图中小正方形的个数为___________(用含
个图中小正方形的个数为___________(用含![]() 的式子表示)
的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,足球场上守门员在O处开出一高球,球从离地面1m的A处飞出(A在y轴上),运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M,距地面约4m高.球第一次落地后又弹起.据试验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
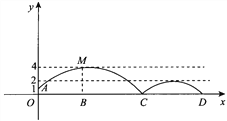
(1)求足球开始飞出到第一次落地时,该抛物线的表达式;
(2)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取![]() ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com