
某农户计划利用现有的一面墙(墙长8米),再修四面墙,建造如图所示的长方体水池,培育不同品种的鱼苗.他已备足可以修高为1.5m、长18m的墙的材料准备施工,设图中与现有一面墙垂直的三面墙的长度都为xm,即AD=EF=BC=xm.(不考虑墙的厚度).
(1)若想水池的总容积为36m3,x应等于多少?
(2)求水池的总容积V与x的函数关系式,并直接写出x的取值范围;
(3)若想使水池的总容积V最大,x应为多少?最大容积是多少?
(1)2或4;(2)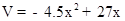 ,x的取值范围是
,x的取值范围是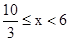 ;(3)当
;(3)当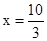 时,总容积V最大=40.
时,总容积V最大=40.
解析试题分析:(1)这个水槽是个长方体,我们先看这个矩形的面积,有了AD、EF、BC的长,因为材料的总长度是18m,因此这个矩形的长应该是18﹣3x,又知道宽为x,又已知了长方体的高,因此可根据长×宽×高=36m3来得出关于x的二次方程从而求出x的值.
(2)和(1)类似,只需把36立方米换成V即可.
(3)此题是求二次函数的最值,可以用配方法或公式法,来求出此时x、y的值.
试题解析:(1)∵AD=EF=BC=x,∴AB=18﹣3x,∴水池的总容积为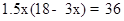 ,即
,即 ,解得:x=2或4,所以x应为2m或4m;
,解得:x=2或4,所以x应为2m或4m;
(2)由(1)知V与x的函数关系式为: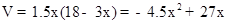 ,∵AB≤8,∴18-3x≤8,解得x≥
,∵AB≤8,∴18-3x≤8,解得x≥ ,x的取值范围是:
,x的取值范围是: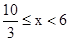 ;
;
(3)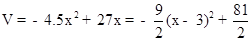 ,∴由函数图象知:当x=3时,V有最大值40.5.∵
,∴由函数图象知:当x=3时,V有最大值40.5.∵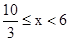 ,∴若使水池的总容积最大,
,∴若使水池的总容积最大,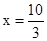 ,最大容积为40m3.
,最大容积为40m3.
考点:1.二次函数的应用;2.应用题.


科目:初中数学 来源: 题型:解答题
已知二次函数 为常数,且
为常数,且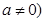 .
.
(1)求证:不论 为何值,该函数的图象与
为何值,该函数的图象与 轴总有两个公共点;
轴总有两个公共点;
(2)设该函数的图象的顶点为C,与 轴交于A,B两点,当△ABC的面积等于2时,求
轴交于A,B两点,当△ABC的面积等于2时,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线y=2x2﹣2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
(1)写出以A,B,C为顶点的三角形面积;
(2)过点E(0,6)且与x轴平行的直线l1与抛物线相交于M、N两点(点M在点N的左侧),以MN为一边,抛物线上的任一点P为另一顶点做平行四边形,当平行四边形的面积为8时,求出点P的坐标;
(3)过点D(m,0)(其中m>1)且与x轴垂直的直线l2上有一点Q(点Q在第一象限),使得以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似,求线段QD的长(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式及顶点D的坐标;
(2)若点P是抛物线第一象限上的一个动点,过点P作PQ∥AC交x轴于点Q.当点P的坐标为 时,四边形PQAC是平行四边形;当点P的坐标为 时,四边形PQAC是等腰梯形. (利用备用图画图,直接写出结果,不写求解过程).
(3)若P为线段BD上的一个动点,过点P作PM⊥x轴于点M,求四边形PMAC的面积的最大值和此时点P的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,黎叔叔想用60m长的篱笆靠墙MN围成一个矩形花圃ABCD,已知墙长MN=30m.
(1)能否使矩形花圃ABCD的面积为400m2?若能,请说明围法;若不能,请说明理由.
(2)请你帮助黎叔叔设计一种围法,使矩形花圃ABCD的面积最大,并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线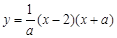
 与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(1)若抛物线过点M(-2,-2),求实数a的值;
(2)在(1)的条件下,解答下列问题:
①求出△BCE的面积;
②在抛物线的对称轴上找一点P,使CP+EP的值最小,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
当抛物线的解析式中含有字母系数时,随着系数中的字母取值的不同,抛物线的顶点坐标也将发生变化.例如:由抛物线y=x2-2mx+m2+2m-1①有y=(x-m)2+2m-1②,
所以抛物线顶点坐标为(m,2m-1),即x=m③,y=2m-1④.
当m的值变化时,x,y的值也随之变化,因而y的值也随x值的变化而变化.
将③代入④,得y=2x-1⑤.可见,不论m取任何实数,抛物线顶点的纵坐标y和横坐标x都满足关系式:y=2x-1;
根据上述阅读材料提供的方法,确定点(-2m, m-1)满足的函数关系式为_______.
(2)根据阅读材料提供的方法,确定抛物线 顶点的纵坐标y与横坐标x之间的关系式.
顶点的纵坐标y与横坐标x之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完,该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润y1(元)与国内销售数量x(千件)的关系为: 若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为:
若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: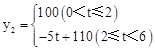
(1)用x的代数式表示t为:t= ;当0<x≤4时, y2与x的函数关系为y2= ;当 ≤x< 时,y2=100;
(2)求每年该公司销售这种健身产品的总利润w(千元)与国内的销售数量x(千件)的函数关系式,并指出x的取值范围;
(3)该公司每年国内、国外的销售量各为多少时,可使公司每年的总利润最大?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线 与
与 轴交于点
轴交于点 .
.
(1)平移该抛物线使其经过点 和点
和点 (2,0),求平移后的抛物线解析式;
(2,0),求平移后的抛物线解析式;
(2)求该抛物线的对称轴与(1)中平移后的抛物线对称轴之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com