练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    图中是抛物线形拱桥，当水面宽AB＝8米时，拱顶到水面的距离CD＝4米．如果水面上升1米，那么水面宽度为多少米？
    .

    试题分析：首先建立平面直角坐标系，设抛物线解析式为y=ax2，进而求出解析式，即可得出EF的长．
    试题解析:如图所示建立平面直角坐标系，

    设抛物线解析式为y=ax2，
    由已知抛物线过点B（4，-4），则-4=a×42，
    解得：a=-，
    ∴抛物线解析式为：y=-x2，
    当y=-3，则-3=-x2，
    解得：x1=2，x2=-2，
    ∴EF=4，
    答：水面宽度为4米．
    考点: 二次函数的应用.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：解答题

    如图，在平面直角坐标系中，二次函数的图象与x轴交于A、B两点，A点在原点的左则，B点的坐标为(3，0)，与y轴交于C(0，―3)点，点P是直线BC下方的抛物线上一动点。

    ⑴求这个二次函数的表达式；
    ⑵连结PO、PC，在同一平面内把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由；
    ⑶当点P运动到什么位置时，四边形ABPC的面积最大，并求出此时P点的坐标和四边形ABPC的最大面积．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    抛物线顶点坐标为点C(1,4),交x轴于点A(3,0)，交y轴于点B.
    (1)求此抛物线的解析式；
    (2)抛物线上是否存在点P,使,若存在，求出P点坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    已知，二次函数的图像经过点和点B，其中点B在第一象限，且OA=OB，cot∠BAO=2．

    （1）求点B的坐标；
    （2）求二次函数的解析式；
    （3）过点B作直线BC平行于x轴，直线BC与二次函数图像的另一个交点为C，联结AC，如果点P在x轴上，且△ABC和△PAB相似，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    已知一个二次函数的顶点A的坐标为（1，0），且图像经过点B（2，3）.
    （1）求这个二次函数的解析式.
    （2）设图像与y轴的交点为C，记，试用表示（直接写出答案）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

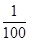    某公司销售一种新型节能电子小产品,现准备从国内和国外两种销售方案中选择一种进行销售:①若只在国内销售,销售价格y（元/件）与月销量x（件）的函数关系式为y＝－x＋150,成本为20元/件,月利润为W内（元）;②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件（a为常数,10≤a≤40）,当月销量为x（件）时,每月还需缴纳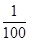x2元的附加费,月利润为W外（元）．
    （1）若只在国内销售,当x＝1000（件）时,y＝         （元/件）;
    （2）分别求出W内、W外与x间的函数关系式（不必写x的取值范围）;
    （3）若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    二次函数y=x2－(m－1)x+4的图像与x轴有且只有一个交点，则m的值为（  ）
    A．1或－3B．5或－3C．－5或3D．以上都不对

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    二次函数y=kx2﹣6x+3的图象与x轴有交点，则k的取值范围是（　　）
    A．k＜3B．k＜3且k≠0
    C．k≤3D．k≤3且k≠0

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

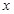    根据下列表格中二次函数y＝ax2＋bx＋c的自变量与函数值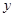的对应值,判断方程ax2＋b x＋c=0（a≠0）的一个解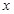的范围是（　 　）　

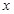    		6．17
    		6．18
    		6．19
    		6．20
    y＝ax2＋bx＋c
    		-0．03
    		-0．01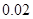


    Ａ．6＜x＜6．17        Ｂ．6．17＜x＜6．18
    Ｃ．6．18＜x＜6．19    Ｄ．6．19＜x＜6．20

    查看答案和解析>>

    同步练习册答案