
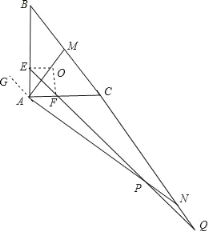
【题目】已知在△ABC中,∠BAC=90°,M是边BC的中点,BC的延长线上的点N满足AM⊥AN.△ABC的内切圆与边AB、AC的切点分别为E、F,延长EF分别与AN、BC的延长线交于P、Q,则![]() =( )
=( )
A. 1B. 0.5C. 2D. 1.5
【答案】A
【解析】
取△ACB的内切圆的圆心是O,连接OE、OF,得出正方形AEOF,求出AE=AF,推出∠AEF=∠AFE=∠CFQ,根据直角三角形斜边上中线性质求出AM=MC,推出∠MCA=∠MAC,根据∠BAC=∠MAG=∠MAN=90°,求出∠GAE=∠MAC=∠MCA,∠EAM=∠CAP,根据三角形的外角性质得出∠GAE=∠APE+∠AEP,∠MCA=∠Q+∠CFQ,求出∠Q=∠NPQ,推出PN=NQ即可.
取△ACB的内切圆的圆心是O,连接OE、OF,作NA的延长线AG,
则OE⊥AB,OF⊥AC,OE=OF,
∵∠BAC=90°,
∴四边形AEOF是正方形,
∴AE=AF,
∴∠AEF=∠AFE,
∵∠BAC=90°,M为斜边BC上中线,
∴AM=CM=BM,
∴∠MAC=∠MCA,
∵∠BAC=90°,AN⊥AM,
∴∠BAC=∠MAG=∠MAN=90°,
∴∠GAE+∠EAM=90°,∠EAM+∠MAC=90°,∠MAC+∠CAN=90°,
∴∠GAE=∠MAC=∠MCA,∠EAM=∠CAP,
∵∠GAE=∠APE+∠AEP,∠MCA=∠Q+∠CFQ,
∵∠AEF=∠AFE=∠CFQ,∠EPA=∠NPQ,
∴∠Q=∠NPQ,
∴PN=QN,
∴![]() =1,
=1,
故选:A.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,AD=3.点E从D向C以每秒1个单位的速度运动,以AE为一边在AE的右下方作正方形AEFG.同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当经过多少秒时.直线MN和正方形AEFG开始有公共点?( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形纸片ABCD中,![]() ,
,![]() ,翻折矩形纸片,使点A落在对角线DB上的点F处,折痕为DE,打开矩形纸片,并连接EF.
,翻折矩形纸片,使点A落在对角线DB上的点F处,折痕为DE,打开矩形纸片,并连接EF.
![]() 的长为多少;
的长为多少;
![]() 求AE的长;
求AE的长;
![]() 在BE上是否存在点P,使得
在BE上是否存在点P,使得![]() 的值最小?若存在,请你画出点P的位置,并求出这个最小值;若不存在,请说明理由.
的值最小?若存在,请你画出点P的位置,并求出这个最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图:
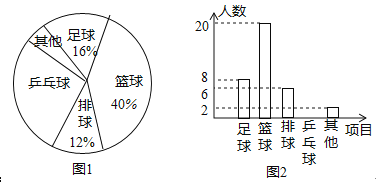
请你根据统计图回答下列问题:
(1)喜欢乒乓球的学生所占的百分比是多少?并请补全条形统计图;
(2)请你估计全校500名学生中最喜欢“排球”项目的有多少名?
(3)在扇形统计图中,“篮球”部分所对应的圆心角是多少度?
(4)篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
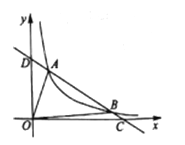
【题目】如图,一次函数y=ax+b与反比例函数![]() (x>0)的图像交于点A(2,5)和点B(m,1).
(x>0)的图像交于点A(2,5)和点B(m,1).
(1)确定这两个函数的表达式;
(2)求出△OAB的面积;
(3)结合图像,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣5ax+c与坐标轴分别交于点A,C,E三点,其中A(﹣3,0),C(0,4),点B在x轴上,AC=BC,过点B作BD⊥x轴交抛物线于点D,点M,N分别是线段CO,BC上的动点,且CM=BN,连接MN,AM,AN.
(1)求抛物线的解析式及点D的坐标;
(2)当△CMN是直角三角形时,求点M的坐标;
(3)试求出AM+AN的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线C1:y=a(x+1)2﹣4的顶点为C,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
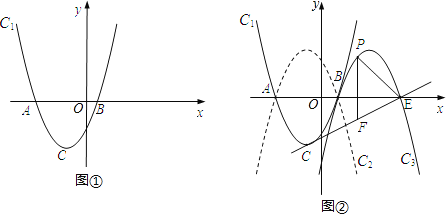
(1)求点C的坐标及a 的值;
(2)如图②,抛物线C2与C1关于x轴对称,将抛物线C2向右平移4个单位,得到抛物线C3.C3与x轴交于点B、E,点P是直线CE上方抛物线C3上的一个动点,过点P作y轴的平行线,交CE于点F.
①求线段PF长的最大值;
②若PE=EF,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com