
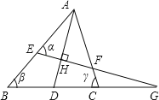
【题目】如图,AD平分∠BAC,EG⊥AD于H,则下列等式中成立的是 ( )
A. ∠α=![]() (∠β﹣∠γ) B. ∠α=
(∠β﹣∠γ) B. ∠α=![]() (∠β+∠γ) C. ∠G=
(∠β+∠γ) C. ∠G=![]() (∠β+∠γ) D. ∠G=
(∠β+∠γ) D. ∠G=![]() ∠α
∠α
【答案】B
【解析】
由于∠α是△BEC的外角,可以得到∠α=∠β+∠G ①,而∠γ是△CFG的外角,可以得到∠γ=∠CFG+∠G ②,而∠AFE和∠CFG是对顶角,由∠AD平分∠BAC,EG⊥AD于H可以推出∠α=∠AFE,然后利用①②即可得到答案.
∵∠α是△BEC的外角,
∴∠α=∠β+∠G①,
∵∠γ是△CFG的外角,
∴∠γ=∠CFG+∠G②
∵AD平分∠BAC,EG⊥AD于H,AH公共边,
∴△AEH≌△AFH,
∴AE=AF,
∴∠α=∠AFE,
而∠AFE=∠CFG,
∴∠AFE=∠CFG=∠α,
∴∠γ=∠α+∠G③,
①③得∠α∠γ=∠β∠α,
∴2∠α=∠β+∠γ,
即∠α=![]() (∠β+∠γ).
(∠β+∠γ).
故选:B.


科目:初中数学 来源: 题型:
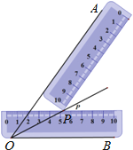
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 三角形三条垂直平分线的交点到三个定点的距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
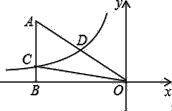
【题目】如图,已知双曲线y=![]() (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,4),则△AOC的面积为( )
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,4),则△AOC的面积为( )
A. 6 B. 12 C. 18 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
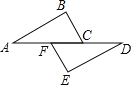
【题目】数学课上,柴老师出了一道题:如图,已知∠A=∠D,∠BCA=∠EFD.要使△ABC≌△DEF,你还应给出的条件是什么?下面四个同学做了回答:小马:“增加∠E=∠B;小李:“增加ED=BA;”小周:“增加AB=EF;”小胡:“增加AF=DC.”针对上面四个同学的回答,你认为正确的是_____.(填上你认为正确的同学的名字)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地农民一直保持着冬种油菜的习惯,利用农闲冬种一季油菜.该地农业部门对2017年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计,并绘制了如下的统计表与统计图(如图):
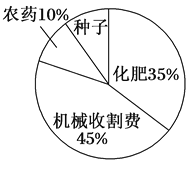
每亩生产成本 | 每亩产量 | 油菜籽市场价格 | 种植面积 |
110元 | 130千克 | 3元/千克 | 500 000亩 |
请根据以上信息解答下列问题:
(1)种植油菜每亩的种子成本是多少元?
(2)农民冬种油菜每亩获利多少元?
(3)2017年该地全县农民冬种油菜的总获利是多少元?(结果用科学记数法表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠C=90°,D为AC上一点,连接BD,将线段BD绕点D顺时针旋转90°得到线段DE,DE与AB相交于点F,过点D作DG⊥AB,垂足为点G.若EF=5,CD=2 ![]() ,则△BDG的面积为 .
,则△BDG的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠C=90°,D为AC上一点,连接BD,将线段BD绕点D顺时针旋转90°得到线段DE,DE与AB相交于点F,过点D作DG⊥AB,垂足为点G.若EF=5,CD=2 ![]() ,则△BDG的面积为 .
,则△BDG的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在新晚报举办的“万人户外徒步活动”中,为统计参加活动人员的年龄情况,从参加人员中随机抽取了若干人的年龄作为样本,进行数据统计,制成如图的条形统计图和扇形统计图(部分). 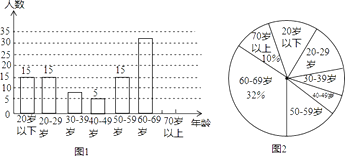
(1)本次活动统计的样本容量是多少?
(2)求本次活动中70岁以上的人数,并补全条形统计图;
(3)本次参加活动的总人数约为12000人,请你估算参加活动人数最多的年龄段的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( ) 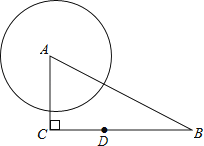
A.1<r<4
B.2<r<4
C.1<r<8
D.2<r<8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com