
 小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min.设小明出发x min后行走的路程为y m.图中的折线表示小明在整个行走过程中y与x的函数关系.
小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min.设小明出发x min后行走的路程为y m.图中的折线表示小明在整个行走过程中y与x的函数关系.分析 (1)观察函数图象,即可得出小明行走的总路程以及途中休息的时间;
(2)根据时间=路程÷速度可求出小丽乘坐缆车需要的时间,设小明在60≤x≤90段的y关于x的函数关系式为y=kx+b,根据图中点的坐标利用待定系数法即可求出该时间段y关于x的函数关系式,代入x=70即可求出y值,再用总路程减去该值即可得出结论.
解答 解:(1)根据图形可得出:小明行走的总路程是3800m;途中休息时间为60-30=30(min).
故答案为:3800;30.
(2)小丽到达缆车终点的时间为3800÷2÷190+60=70(min),
设小明在60≤x≤90段的y关于x的函数关系式为y=kx+b,
将(60,2000)、(90,3800)代入y=kx+b中,得:
$\left\{\begin{array}{l}{2000=60k+b}\\{3800=90k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=60}\\{b=-1600}\end{array}\right.$,
∴小明在60≤x≤90段的y关于x的函数关系式为y=60x-1600.
当x=70时,y=60×70-1600=2600,
此时小明离缆车终点的路程是3800-2600=1200(m).
故答案为:1200.
点评 本题考查了函数的图象以及待定系数法求函数解析式,根据图中点的坐标利用待定系数法求出函数解析式是解题的关键.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
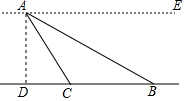 如图,一搜救船在海面A处测得亚航失事客机的第一个黑匣子的俯角∠EAC为60°,第二个黑匣子的俯角∠EAB为30°,此处海底的深度AD为3千米.求两个黑匣子的距离BC的长?(取$\sqrt{3}$≈1.73,精确到0.1千米)
如图,一搜救船在海面A处测得亚航失事客机的第一个黑匣子的俯角∠EAC为60°,第二个黑匣子的俯角∠EAB为30°,此处海底的深度AD为3千米.求两个黑匣子的距离BC的长?(取$\sqrt{3}$≈1.73,精确到0.1千米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
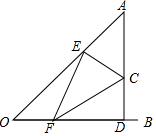 如图,∠AOB=45°,点C在∠AOB内部,CD⊥OB于点D,CD=5,OD=13,点E、点F分别是射线OA、射线OB上的动点,那么FE+FC的最小值是9$\sqrt{2}$.
如图,∠AOB=45°,点C在∠AOB内部,CD⊥OB于点D,CD=5,OD=13,点E、点F分别是射线OA、射线OB上的动点,那么FE+FC的最小值是9$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 最高气温(℃) | 12 | 8 | 11 | 10 | 9 | 8 | 12 |
| 最低气温(℃) | 5 | -1 | -2 | 3 | 0 | -2 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com