
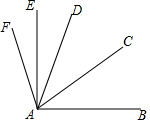
 如图,∠FAB=106°,AE是∠FAD的平分线,AC是∠DAB的平分线,∠EAD=20°.下列关系错误的是( )
如图,∠FAB=106°,AE是∠FAD的平分线,AC是∠DAB的平分线,∠EAD=20°.下列关系错误的是( )| A. | ∠FAD=40° | B. | ∠CAB=33° | C. | ∠FAB=2∠EDC | D. | ∠EAD与∠DAB互余 |
分析 由AE是∠FAD的平分线,得到∠EAF=∠DAE=20°,∠DAF=2∠DAE=40°,故A正确;于是得到∠EAD+∠DAB=86°,故D错误;由AC是∠DAB的平分线,得到∠CAB=∠CAD=$\frac{1}{2}∠$BAD=33°,故B正确;求得∠CAE=∠DAE+∠CAD=53°,于是得到∠FAB=2∠EDC,故③正确.
解答 解:∵AE是∠FAD的平分线,
∴∠EAF=∠DAE=20°,∠DAF=2∠DAE=40°,故A正确;
∴∠BAE=∠FAB-∠EAF=86°,∠BAD=66°,
∴∠EAD+∠DAB=86°,故D错误;
∵AC是∠DAB的平分线,
∴∠CAB=∠CAD=$\frac{1}{2}∠$BAD=33°,故B正确;
∴∠CAE=∠DAE+∠CAD=53°,
∴∠FAB=2∠EDC,故③正确;
故选D.
点评 本题考查了余角和补角,角平分线的定义,熟练掌握角平分线的定义是解题的关键.


科目:初中数学 来源: 题型:解答题
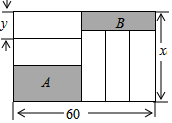 如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影 A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为 y(cm).
如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影 A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为 y(cm).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com