练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．某工厂要招聘A、B两个工种的工人120人，A、B两个工种的工人的月工资分别为1500元和3000元，现要求B工种的人数不少于A工种人数的2倍，要使工厂每月所付的工资总额最少，那么工厂招聘A种工人的人数至多是（　　）人．
    A．50B．40C．30D．20

    分析 题中不等关系是：A，B两种工种的工人共120人，B工种的人数不少于A工种人数的2倍，据此列出不等式组并解答，求出总工资最少时A工种的工人数．

    解答 解：设每月所支付的工资为y元，招聘A工种工人x人，则招聘B工种工人（120-x）人，根据题意得
    y=1500x+3000（120-x）=-1500x+360 000，
    由题意得120-x≥2x，
    解得：x≤40，
    y=-1500x+360 000中的y随x的增大而减少，
    所以当x=40时，y取得最小值300000．
    即当招聘A工种工人40人时，可使每月所付工资最少．
    故选：B．

    点评 本题主要考查对于一元一次不等式的应用以及一次函数的应用，找好题中的不等关系是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    9．下列运算中正确的是（　　）
    A．2x3•x2=2x6B．（x2y）3=x6y3C．（2）-1=-2D．x8÷x2=x4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算：
    （1）-1+5÷（-$\frac{1}{4}$）×4；
    （2）32×（-$\frac{1}{3}$）+8÷（-2）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，CA=CB，CD=CE，∠ACB=∠DCE=α，连AD，BE相交于H，连CH
    （1）如图1，当α=60°时，求∠AHE与∠BHC；
    （2）如图2，当α=90°时，求∠AHE与∠BHC；
    （3）如图3，当α为锐角时，求∠AHE与∠BHC；
    （4）如图4，当α为钝角时，求∠AHE与∠BHC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．我们规定以下三种变换：
    （1）f（a，b）=（-a，b）．如：f（1，3）=（-1，3）；
    （2）g（a，b）=（b，a）．如：g（1，3）=（3，1）；
    （3）h（a，b）=（-a，-b）．如：h（1，3）=（-1，-3）．
    按照以上变换有：f（g（2，-3））=f（-3，2）=（3，2），
    求f（h（5，-3））=（　　）
    A．（5，-3）B．（-5，3）C．（5，3）D．（3，5）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．一宾馆有二人间、三人间、四人间三种客房供游客租住，某旅行团15人准备同时租用这三种客房共5间，如果每个房间都住满，租房方案有（　　）
    A．4种B．3种C．2种D．1种

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

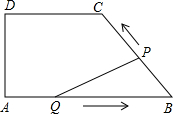    3．如图，在四边形ABCD中，DC∥AB，AD=4，DC=5，AB=8．如果点P由B点出发沿BC方向向点C匀速运动，同时点Q由A点出发沿AB方向向点B匀速运动，它们的速度均为每秒1个单位长度．当P点到达C点时，两点同时停止运动，连接PQ．设运动时间为t秒，当△PQB为等腰三角形时，t的值为$\frac{40}{11}$、$\frac{48}{11}$或4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．小明有5张写着不同数字的卡片：

    请你分别从中取出2张卡片，使这2张卡片上的数字
    （1）相加的和最小，列式并计算出结果；
    （2）相乘的积最大，列式并计算出结果；
    （3）进行加或乘或除或乘方运算使得结果最大，列式并计算出结果．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

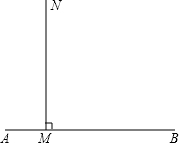    1．已知如图：射线MN⊥AB于点M，点C从M出发，以1cm/s的速度沿射线MN运动，AM=1，MB=4，设运动时间为ts，①当△ABC为等腰三角形时，求t的值；②当△ABC为直角三角形时，求t的值；③点C在运动的过程中，若△ABC为钝角三角形，则t的取值范围是0＜t＜2；若△ABC为锐角三角形，则t的取值范围是t＞2．

    查看答案和解析>>

    同步练习册答案