
����Ŀ��������y����x2+x+b��x�ύ��A��B���㣬��y�ύ�ڵ�C��
��1����B��������2��0��
����ʵ��b��ֵ��
����ͼ1����E���������ڵ�һ�����ڵ�ͼ���ϵĵ㣬���CBE��������ֵ����ʱ��E�����꣮
��2����ͼ2�������ߵĶԳ��ύx���ڵ�D�����������ϴ��ڵ�P��ʹ��P��B��C��D�ĵ��ܹ���ƽ���ı��Σ���ʵ��b��ֵ������ʾ������M��N������ΪM��x��y����N��x��y�������߶�MN���е�����Ϊ��![]() ��
��![]() ��
��

���𰸡���1����b��2���ڡ�CBE��������ֵΪ1����ʱE��1��2������2��b����1+![]() ��b��
��b��![]() ����
����![]() ��
��![]() ��
��
��������
��1��������B��2��0������y����x2+x+b������b��
����E��m����m2+m+2�������BC��ֱ�߽���ʽΪy����x+2������E��BC��ֱ��ֱ�߽���ʽΪy��x��m2+2�������ֱ�߽���F����EF���ʱ����CBE��������
��2������C��0��b����B��![]() ��0������M��t����t2+t+b�������öԽ�����ƽ�ֵ��ı�����ƽ���ı��Σ�������������⣺����CM��BDΪƽ���ı��εĶԽ���ʱ��
��0������M��t����t2+t+b�������öԽ�����ƽ�ֵ��ı�����ƽ���ı��Σ�������������⣺����CM��BDΪƽ���ı��εĶԽ���ʱ��![]() ��
��![]() ��
��![]() ��0�����b����1+
��0�����b����1+![]() ������BM��CDΪƽ���ı��εĶԽ���ʱ��
������BM��CDΪƽ���ı��εĶԽ���ʱ��![]() ��
��![]() ��
��![]() ��
��![]() ��b�⣻����BC��MDΪƽ���ı��εĶԽ���ʱ��
��b�⣻����BC��MDΪƽ���ı��εĶԽ���ʱ��![]() ��
��![]() ��
��![]() ��
��![]() �����b��
�����b��![]() ��b����
��b����![]() ���ᣩ��
���ᣩ��
�⣺��1��������B��2��0������y����x2+x+b��
�õ�0����4+2+b��
��b��2��
��C��0��2����B��2��0����
��BC��ֱ�߽���ʽΪy����x+2��
��E��m����m2+m+2����
����E��BC��ֱ��ֱ�߽���ʽΪy��x��m2+2��
��ֱ��BC���䴹�ߵĽ���ΪF��![]() ����
����![]() +2����
+2����
��EF��![]() ����
����![]() +2����
+2����![]() [��
[��![]() ��m��1��2+
��m��1��2+![]() ]��
]��
��m��1ʱ��EF�����ֵ![]() ��
��
��S��![]() ��BC��EF��
��BC��EF��![]() ��2
��2![]() ��
��![]() ��1��
��1��
���CBE��������ֵΪ1����ʱE��1��2����
��2���������ߵĶԳ���Ϊx��![]() ��
��
��D��![]() ��0����
��0����
��������x�����������㣬
�����1+4b��0��
��b����![]() ��
��
��C��0��b����B��![]() ��0����
��0����
��M��t����t2+t+b����
����CM��BDΪƽ���ı��εĶԽ���ʱ��
C��M���е�Ϊ��![]() ��
��![]() ����B��D���е�Ϊ��
����B��D���е�Ϊ��![]() ��0����
��0����
��![]() ��
��![]() ��
��![]() ��0��
��0��
��ã�b����1+![]() ��b����1��
��b����1��![]() ����ȥ����
����ȥ����
��b����1+![]() ��
��
����BM��CDΪƽ���ı��εĶԽ���ʱ��
B��M���е�Ϊ��![]() ��
��![]() ����C��D���е�Ϊ��
����C��D���е�Ϊ��![]() ��
��![]() ����
����
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��b�⣻
����BC��MDΪƽ���ı��εĶԽ���ʱ��
B��C���е�Ϊ��![]() ��
��![]() ����M��D���е�Ϊ��
����M��D���е�Ϊ��![]() ��
��![]() ����
����
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��ã�b��![]() ��b����
��b����![]() ���ᣩ��
���ᣩ��
����������b����1+![]() ��b��
��b��![]() ��
��


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ������1�³���20000Ԫ/Ķ�ļ۸�а���10Ķ��������ֲijũ�����֪������ͳ��ֲ��ÿ��ÿĶ�ܲ���3000ǧ�ˣ�ÿĶ����ֲ����Ϊ2500Ԫ��������ѧ��ֲ��ÿ��ÿĶ����������![]() ������ֲ���û�����2000Ԫ/Ķ����ǰ����Ҫ��Ͷ��25��Ԫ������4���µ�ʱ��������������ĸ��ƣ������ڼ�����ֲ����֪ÿǧ��ũ�����г��ۼ�Ϊ3Ԫ��ÿ�µ�һ����ȫ�����ۣ�����ǰ
������ֲ���û�����2000Ԫ/Ķ����ǰ����Ҫ��Ͷ��25��Ԫ������4���µ�ʱ��������������ĸ��ƣ������ڼ�����ֲ����֪ÿǧ��ũ�����г��ۼ�Ϊ3Ԫ��ÿ�µ�һ����ȫ�����ۣ�����ǰ![]() ���������ܶ�Ϊ
���������ܶ�Ϊ![]() ����Ԫ����
����Ԫ����
��1����![]() ʱ���ֱ����������ֲ�����µ������ܶ�
ʱ���ֱ����������ֲ�����µ������ܶ�![]() ��
��
��2���ʣ�����ũ��ѡ���ѧ��ֲ�������º��ܹ��ջسɱ���
��3���ڣ�2���������£������2019��1�³�������ô����Ҫ����ʱ����ũ����õ��������ܹ�������ͳ��ֲͬ��ʱ��������õ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����ٽ�����⣮
��ȱ��Σ��Ǵ���ʽ��ֵ��һ������Ҫ�ķ��������ú�ȱ��Σ���������������ת��Ϊ���������㣬���Ѵ����ϸߵĴ���ʽת��Ϊ�����ϵ͵Ĵ���ʽ���統x��![]() ʱ����
ʱ����![]() ��x2��x+2��ֵ��Ϊ������⣬��ֱ�Ӱ�x��
��x2��x+2��ֵ��Ϊ������⣬��ֱ�Ӱ�x��![]() ���������ʽ�У����м��㣬��Ȼ���鷳�����ǿ���ͨ����ȱ��Σ��Ա�����н��
���������ʽ�У����м��㣬��Ȼ���鷳�����ǿ���ͨ����ȱ��Σ��Ա�����н��
����һ�����������Σ���x��![]() ����x��1��
����x��1��![]() ���ٰ�����Ĵ���ʽ����Ϊ���ڣ�x��1���ı���ʽ��
���ٰ�����Ĵ���ʽ����Ϊ���ڣ�x��1���ı���ʽ��
ԭʽ��![]() ��x3��2x2��2x��+2
��x3��2x2��2x��+2
��![]() [x2��x��1����x��x��1����3x]+2
[x2��x��1����x��x��1����3x]+2
��![]() [x��x��1��2��3x]+2
[x��x��1��2��3x]+2
��![]() ��3x��3x��+2
��3x��3x��+2
��2
���������Ƚ�����������ʽ���ٰѵ�ʽ����ͬʱƽ����������������ת��Ϊ���������㣮��x��1��![]() ���ɵ�x2��2x��2��0������x2��2x��2��x2��2x+2��
���ɵ�x2��2x��2��0������x2��2x��2��x2��2x+2��
ԭʽ��![]() x��2x+2����x2��x+2
x��2x+2����x2��x+2
��x2+x��x2��x+2
��2
������ϵĽ�������˼·�ͷ���������������⣺
��1����a2��3a+1��0����2a3��5a2��3+![]() ��ֵ��
��ֵ��
��2����֪x��2+![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
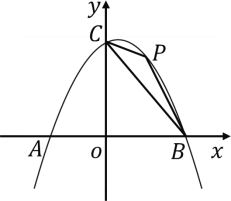
����Ŀ����ͼ��������![]() ��
��![]() ����A����3��0����B���㣬��y�ύ�ڵ�C
����A����3��0����B���㣬��y�ύ�ڵ�C![]() ������AC��BC����P���߶�BC�Ϸ��������ϵ�һ�����㣬��P�ĺ�����Ϊ
������AC��BC����P���߶�BC�Ϸ��������ϵ�һ�����㣬��P�ĺ�����Ϊ![]() ��
��
��1����������ߵı���ʽ��
��2������![]() ����MA+MB����Сֵ���������ʱ��M�����꣮
����MA+MB����Сֵ���������ʱ��M�����꣮
��3����![]() ��������ֵ���������ʱ��P�����꣮
��������ֵ���������ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����ABΪֱ���ġ�O��BC�ڵ�D������D��EF��AC�ڵ�E����AB���ӳ����ڵ�F��
��1���ж�ֱ��DE���O��λ�ù�ϵ����˵�����ɣ�
��2�����AB=5��BC=6����DE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
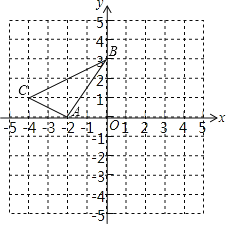
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�A����2��0����B��0��3����C����4��1������ԭ��OΪ��ת���ģ�����ABC˳ʱ����ת90��õ���A'B'C'�����е�A��B��C��ת��Ķ�Ӧ��ֱ�Ϊ��A'��B'��C'��
��1��������A'B'C'����д����A'��B'��C'�����ꣻ
��2������B'��B��A����������߶�Ӧ�ĺ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������Ϊ3����Ϊ8�ij�����������������ˮƽ�����ϣ�����ʢ��ˮ��ˮ���Ϊ6���Ƶ���һ�ⳤ������ת��б��ˮ��ǡ�ô��������ڱ�Ե��ͼ2�Ǵ�ʱ��ʾ��ͼ����ͼ2��ˮ��߶�Ϊ�� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ҫ�ڳ����θְ�ABCD�ı�AB����һ��E��ʹ��AEC��150����Ӧ����ȷ����E��λ�ã�Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
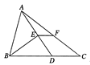
����Ŀ����ͼ����![]() �У�����
������![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ��ƽ����
��ƽ����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ���е㣬����
���е㣬����![]() .���ı���DCFE�͡�BDE�������Ϊ3�����ABC�����Ϊ____.
.���ı���DCFE�͡�BDE�������Ϊ3�����ABC�����Ϊ____.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com