
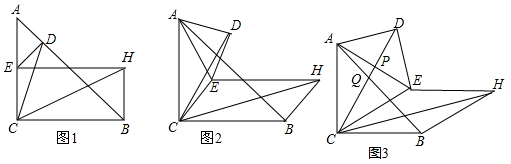
���� ��1�����ۣ�CH=$\sqrt{2}$CD����ͼ1�У���DM��AC��M��DN��EH��N������֤����CMD�ա�HND���Ƴ���DCH�ǵ���ֱ�������μ��ɽ�����⣻
��2�����ۣ�CH=$\sqrt{2}$CD����ͼ1�У���DM��AC��M��DN��EH��N������֤����ADM�ա�EDN����֤����CMD�ա�HND���Ƴ���DCH�ǵ���ֱ�������μ��ɽ�����⣻
��3����ͼ3�У���ACE����Ϊ�ȱ������Σ���CA=CE��DA=DE���Ƴ�CD��ֱƽ��AE����ACP=��ECP=30�㣬�Ƴ�DP=AP=PE����DP=AP=PE=a����AC=CE=AE=2a��CP=$\sqrt{3}$a����QM��AC��M����AM=QM=x����CM=$\sqrt{3}$MQ=$\sqrt{3}$x��CQ=2x�����CQ��PQ����a��ʾ�������ɽ�����⣻
��� �⣺��1�����ۣ�CH=$\sqrt{2}$CD��
���ɣ���ͼ1�У���DM��AC��M��DN��EH��N��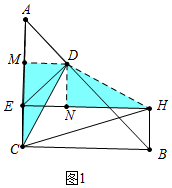
���ı���BCEH�Ǿ��Σ�
��EH=BC����CEH=��MEN=��DME=��DNE=90�㣬
���ı���DMEN�Ǿ��Σ�
�ߡ�ADE�ǵ���ֱ�������Σ�
��DM=ME=AM��
���ı���DMEN�������Σ�
��DN=DM=EM=AM��
��AC=BC=EH��
��CM=HN���ߡ�CMD=��DNH=90�㣬
���CMD�ա�HND��
��CD=DH����CDM=��HDN��
���MDN=��CDH=90�㣬
���CDH�ǵ���ֱ�������Σ�
��CH=$\sqrt{2}$CD��
��2����ͼ2�У����ۣ�CH=$\sqrt{2}$CD��
���ɣ���ͼ1�У���DM��AC��M��DN��EH��N��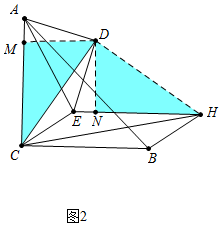
�ߡ�ADE=��MDN=90�㣬
���ADM=��EDN��
��AD=DE����AMD=��DNE=90�㣬
���ADM�ա�EDN��
��DM=DN��AM=EN��
��AC=BC=EH��
��CM=HN���ߡ�CMD=��DNH=90�㣬
���CMD�ա�HND��
��CD=DH����CDM=��HDN��
���MDN=��CDH=90�㣬
���CDH�ǵ���ֱ�������Σ�
��CH=$\sqrt{2}$CD��
��3����ͼ3�У���ACE����Ϊ�ȱ������Σ�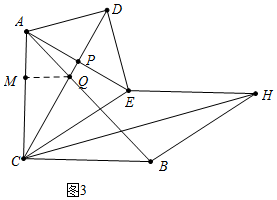
��CA=CE��DA=DE��
��CD��ֱƽ��AE����ACP=��ECP=30�㣬
��DP=AP=PE����DP=AP=PE=a����AC=CE=AE=2a��CP=$\sqrt{3}$a��
��QM��AC��M����AM=QM=x����CM=$\sqrt{3}$MQ=$\sqrt{3}$x��CQ=2x��
��x+$\sqrt{3}$x=2a��
��x=��$\sqrt{3}$-1��a��
��CQ=��2$\sqrt{3}$-2��a��
��PQ=PC-CQ=$\sqrt{3}$a-��2$\sqrt{3}$-2��a=��2-$\sqrt{3}$��a��
��$\frac{DP}{QP}$=$\frac{a}{��2-\sqrt{3}��a}$=2+$\sqrt{3}$��
�ʴ�Ϊ2+$\sqrt{3}$��
���� ���⿼��ȫ�������ε��ж������ʡ�����ֱ�������ε����ʡ���ת�任��ƽ���ı��ε����ʵ�֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ�����ȫ�������ν�����⣬ѧ�����ò���������⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ac��bc | B�� | |a-b|=a-b | C�� | -a��-b��c | D�� | -a-c��-b-c |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
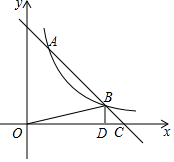 ��ͼ��ֱ��y=-x+5��˫����y=$\frac{k}{x}$��x��0���ཻ��A��B���㣬��x�ύ�ڵ�C������B��BD��x���ڵ�D����BDC�������$\frac{1}{2}$����k��ֵΪ��������
��ͼ��ֱ��y=-x+5��˫����y=$\frac{k}{x}$��x��0���ཻ��A��B���㣬��x�ύ�ڵ�C������B��BD��x���ڵ�D����BDC�������$\frac{1}{2}$����k��ֵΪ��������| A�� | 3.5 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
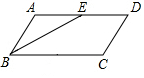 ��ͼ����ƽ���ı���ABCD�У�E��AD���ϵ��е㣮����ABE=��EBC��AB=2����ƽ���ı���ABCD���ܳ���12��
��ͼ����ƽ���ı���ABCD�У�E��AD���ϵ��е㣮����ABE=��EBC��AB=2����ƽ���ı���ABCD���ܳ���12���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
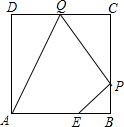 ��ͼ����֪������ABCD�߳�Ϊ3����E��AB������BE=1����P��Q�ֱ��DZ�BC��CD�Ķ��㣨�����붥���غϣ������ı���AEPQ���ܳ�ȡ��Сֵʱ���ı���AEPQ�������$\frac{9}{2}$��
��ͼ����֪������ABCD�߳�Ϊ3����E��AB������BE=1����P��Q�ֱ��DZ�BC��CD�Ķ��㣨�����붥���غϣ������ı���AEPQ���ܳ�ȡ��Сֵʱ���ı���AEPQ�������$\frac{9}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com