
 如图,点P从点A出发沿着线段AB向点B匀速运动,点P出发4分钟时距A地240cm,此时点Q也从点A沿着线段AB向点B匀速运动,再经过6分钟点Q追上点P,又经过2分钟点Q到达点B处,此时点P、Q同时停止运动,设点P的运动时间为t分钟.
如图,点P从点A出发沿着线段AB向点B匀速运动,点P出发4分钟时距A地240cm,此时点Q也从点A沿着线段AB向点B匀速运动,再经过6分钟点Q追上点P,又经过2分钟点Q到达点B处,此时点P、Q同时停止运动,设点P的运动时间为t分钟.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
| A、2000×108 |
| B、2×1011 |
| C、0.2×1012 |
| D、20×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| AF |
| AC |
| 1 |
| 2 |
| 1 |
| 1+1 |
| AO |
| AD |
| 2 |
| 3 |
| 2 |
| 2+1 |
| AF |
| AC |
| 1 |
| 3 |
| 2 |
| 2+1 |
| AO |
| AD |
| 2 |
| 4 |
| 2 |
| 2+2 |
| AF |
| AC |
| 1 |
| 4 |
| 1 |
| 1+3 |
| AO |
| AD |
| 2 |
| 5 |
| 2 |
| 2+3 |
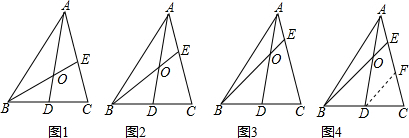
| AE |
| AC |
| 1 |
| 1+n |
| AO |
| AD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com