
分析 (1)设购进A种LED节能灯x盏,根据“投入资金不超过6900元”列方程求解可得;
(2)设购进A种LED节能灯a盏,则购进B种LED节能灯(200-a)盏,根据“投入资金不超过6900元,且销售完这批LED节能灯后获利不少于2600元”列不等式组求得a的范围,根据a为整数解知购进方案,求得每种方案的利润,比较后即可知.
解答 解:(1)设购进A种LED节能灯x盏,
根据题意,得
18x+45(200-x)≤6900,
解得x≥77$\frac{7}{9}$.
因为x是正整数,
所以x=78.
答:店至少购进A型节能灯78盏;
(2)设购进A种LED节能灯a盏,则购进B种LED节能灯(200-a)盏,
根据题意,得:$\left\{\begin{array}{l}{18a+45(200-a)≤6900}\\{10a+15(200-a)≥2600}\end{array}\right.$,
解得:77$\frac{7}{9}$≤a≤80,
∵a为整数,
∴购货方案有如下三种:
①购进A种LED节能灯78盏,则购进B种LED节能灯122盏,此时获利为:78×10+122×15=2610(元);
②购进A种LED节能灯79盏,则购进B种LED节能灯121盏,此时获利为:79×10+121×15=2605(元);
③购进A种LED节能灯80盏,则购进B种LED节能灯120盏,此时获利为:80×10+120×15=2600(元);
故方案①获利最大,最大值为2610元.
点评 本题主要考查二元一次不等式组和一元一次不等式组的实际应用,理解题意找到题目中蕴含的相等关系或不等关系从而列出方程组或不等式组是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
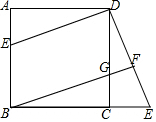 已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=AH,连接BG并延长交DE于F.
已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=AH,连接BG并延长交DE于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
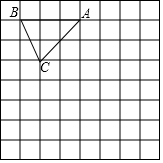 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位,再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°,得到△A1B2C2.
如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位,再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°,得到△A1B2C2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 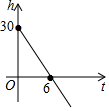 | B. | 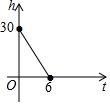 | C. | 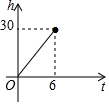 | D. | 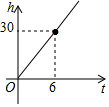 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
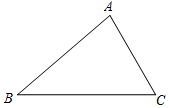 已知△ABC,请按要求完成画图、说明画图过程及画图依据.
已知△ABC,请按要求完成画图、说明画图过程及画图依据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
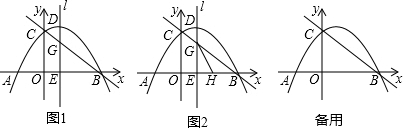
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com