
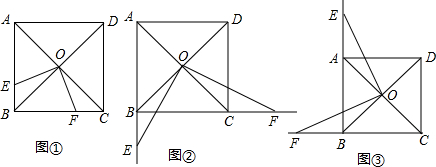
分析 如图①由正方形ABCD的对角线交于点O,根据正方形的性质得到∠BOC=90°,又因为∠EOF=90°,得到∠1+∠2=90°,∠2+∠3=90°,证得∠1=∠3,
由正方形的性质得到∠4=∠5=45°,BO=CO,证得△BOE≌△COF,得到对应边相等由等量代换得到结论;
(1)的解题思路与以上相同;
(2)由AB2+CA2=24,解得AB=2$\sqrt{2}$,根据S△BOF=6,求得BF,根据图①和图③分两种情况求解.
解答  证明:如图①,∵正方形ABCD的对角线交于点O,
证明:如图①,∵正方形ABCD的对角线交于点O,
∴∠BOC=90°,
∵∠EOF=90°,
∴∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
∵∠4=∠5=45°,BO=CO,
在△BOE与△COF中,
$\left\{\begin{array}{l}{∠1=∠3}\\{OB=OC}\\{∠4=∠5}\end{array}\right.$,
∴△BOE≌△COF,
∴BE=CF,
∴BE+BF=BF+CF=BC,
即BE+BF=BC;
(1)如图②,∵正方形ABCD的对角线交于点O,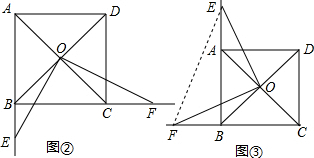
∴∠BOC=90°,
∵∠EOF=90°,
∴∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
∵OB=OC,∠OBE=∠OCF=135°,
在△BOE与△COF中,
$\left\{\begin{array}{l}{∠1=∠3}\\{OB=OC}\\{∠OBE=∠OCF}\end{array}\right.$,
∴△BOE≌△COF,
∴BE=CF,
∴BE=BF-BC;
(2)EF=2$\sqrt{26}$,10$\sqrt{2}$,
如图③,连接EF,
∵AB2+CA2=24,
又∵AC2=2AB2,
∴AB=2$\sqrt{2}$,
∵S△BOF=6,
∴BF=6$\sqrt{2}$,
由(1)证得AE=BF=6$\sqrt{2}$,
∴BE=8$\sqrt{2}$,
在RT△BEF中,
EF=$\sqrt{{BF}^{2}{+BE}^{2}}$=10$\sqrt{2}$,
如图①EF=$\sqrt{{BF}^{2}{+BE}^{2}}$=2$\sqrt{26}$.
故答案为:10$\sqrt{2}$,2$\sqrt{26}$.
点评 本题考查了全等三角形的判定与性质,正方形的性质,勾股定理的应用,注意(2)中不要漏解.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,以△ABC三边为边在BC的同一侧分别作3个等边三角形,即△ABD、△BCE、△ACF.四边形AFED一定是平行四边形吗?如果是,请说明理由.
如图,以△ABC三边为边在BC的同一侧分别作3个等边三角形,即△ABD、△BCE、△ACF.四边形AFED一定是平行四边形吗?如果是,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知二次函数y=ax2+2x+3的图象与x轴交于点A、点B(点B在X轴的正半轴上),与y轴交于点C,其顶点为D,又tan∠OBC=1,过点A任作直线l交线段BD于点P,若点B、D到直线l的距离分别记为d1、d2,则d1+d2的最大值为$\sqrt{5}$.
如图,已知二次函数y=ax2+2x+3的图象与x轴交于点A、点B(点B在X轴的正半轴上),与y轴交于点C,其顶点为D,又tan∠OBC=1,过点A任作直线l交线段BD于点P,若点B、D到直线l的距离分别记为d1、d2,则d1+d2的最大值为$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是跷跷板的示意图,立柱OC与地面垂直.以O为横板AB的中点,AB绕点O上下转动,横板AB的B端最大高度h是否会随横板长度的变化而变化呢?一位同学做了如下研究:他先设AB=2m,OC=0.5m,通过计算得到此时的h1,再将横板AB换成横板A′B′,O为横板A′B′的中点,且A′B′=3m,此时B′点的最大高度为h2,由此得到h1与h2的大小关系是:h1=h2(填“>”、“=”或“<”).可进一步得出h随横板的长度的变化为不变(填“不变”或“改变”)
如图是跷跷板的示意图,立柱OC与地面垂直.以O为横板AB的中点,AB绕点O上下转动,横板AB的B端最大高度h是否会随横板长度的变化而变化呢?一位同学做了如下研究:他先设AB=2m,OC=0.5m,通过计算得到此时的h1,再将横板AB换成横板A′B′,O为横板A′B′的中点,且A′B′=3m,此时B′点的最大高度为h2,由此得到h1与h2的大小关系是:h1=h2(填“>”、“=”或“<”).可进一步得出h随横板的长度的变化为不变(填“不变”或“改变”)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com